Reference no: EM1318744

Question: From this point on we will not concern ourselves with the fact that the set of all permutations over Ω forms a group. We will be focusing on individual permutations.

There is another very useful way to describe permutations. We denote by {a1, a2,.......ak} a cycle of k elements. This cycle defines a permutation ρ{a1} = a1, ρ{a2} = a2,...........,ρ{ak-1} = ak and also ρ{ak} = a1. A product of two cycles corresponding to the composition {as functions} of the two corresponding permutation. For example, consider the permutation ρ = {1 2 3}{2 4}, defined as a composition - apply first the rightmost one - of two cycles. Suppose that we wish to find ρ{4} we have that fist 4 goes to 2 in the right cycles. Then, 2 go to 3. Therefore, ρ{4} = 3. How about ρ{1}? The second cycle is not concerned at all with 1 hence, ρ{1} = 2. As another example consider a permutation defined by the product { 1 2 3 4 X 4 5 6 7}{8 9}. Clearly, every product of one or more cycles defines a permutation. The other direction is also true. Actually, given any permutation can we always write it as a product of disjoint cycles? Two cycles are disjoint if they don't have any common element. Such a thing is called cycle-decomposition of the permutation. One of the first theorems for permutations says that

Theorem: Every permutation r over Ω can be written as a product of disjoint cycles. The main focus of this question is to prove this theorem.

For example, consider the permutation we had before:

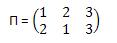
Observe that if we start from 1 we can go to 2 and then from 2 we can go back to 1 and this repeats forever. Also, 3 goes to 3 and then again. Hence, we can write r is r = {1 2}{3}. That is, 1,2 appeared only in one cycle, and 3 only in one. Actually, for notational simplicity we can omit cycles that are identities on certain elements, since this is well-understood. Hence, we could about notation and write r = {1 2}. Also note that indeed those cycles are disjoint.

You will prove this theorem by showing that for every permutation given in the input {r{1},........,r{n}} you can construct in the output the cycle-decomposition of this permutation. That is, your proof will give us for free an algorithm to actually solve this problem in practice.

[A] Define the problem where given the permutation we construct cycle decomposition and give at least two examples of input-outputs. Give an algorithm for the problem.

[B] Prove that your algorithm is correct for the problem.