Reference no: EM132784762

MAE 3403 Computer Methods in Analysis and Design - Oklahoma State University

You will write four Python programs named hw2a.py, hw2b.py, hw2c.py and hw2d.py. Those programs will fulfill all of the requirements given in parts a, b, c, and d below. You will place those four python files into a single compressed file named hw2.zip. You will upload hw2.zip to the Homework 2 dropbox.

You will test your functions and using the particular numerical values and functions given.When we grade your assignment, we will run your program with those given numerical values, looking for correct answers. Then we will change the numerical values (including changing the SIZES of the arrays) and look for correct answers for those modified values as well. We will only use numerical values, array sizes and functions that make sense. We will not be testing your program to see how it handles bad data.

In this assignment, you must use variables, loops, if statements, your own function definitions and function calls to write the required functions. For now, you may not use any of the powerful functions available in python modules, with two exceptions: you may import functions from the math module and the copy module.

You must include reasonable comments in your code.

See your MAE 3013 textbook and the MAE 3013 Equation Sheet for a reminder of:

The Secant Method for finding the solution (root or zero) or a nonlinear equation
The Simpson's 1/3 rule for numerical integration
The Gauss-Jordanelimination method for finding an inverse matrix.

a) Write a function defined as: defProbability(PDF,args,c, GT=True):

PDF: is the Gaussian/normal probability density function f(x) = (1/(σ√2Π)).e^{-1/2(x-μ/σ)2}, which takes 1 argument containing values for x, μ (population mean), and σ (population standard deviation).
args: is a tuple containing μ and σ
c: is a floating point value
GT: is a boolean indicating if we want the probability of x being greater than c (GT=True) or less than c (GT=False)

To find the probability of x<c you should use the Simpson's 1/3 rule to integrate PDF between the limits of x=-5⋅σ to c.

Write and call a main() function that uses your Probability function to find:
P(x<1|N(0,1)): probability x<1 given a normal distribution of x with μ=0, σ=1
P(x>μ+2σ|N(175, 3))
Print you findings to the console in the following format:
P(x<1.00|N(0,1))=Y.YY
P(x>181.00|N(175,3))=Z.ZZ

b) Write a function defined as: def Secant(fcn, x0, x1, maxiter=10, xtol=1e-5):

Purpose: use the Secant Method to find the root of fcn(x), in the neighborhood of x0 and x1.

fcn: the function for which we want to find the root
x0 and x1: two x values in the neighborhood of the root
xtol: exit if the |xnewest- xprevious| <xtol
maxiter: exit if the number of iterations (new x values) equals this number
return value: the final estimate of the root (most recent new x value)

Write and call a main() function that uses your Secant function to estimate and print the solution of:
x-3cos(x)=0; with x0=1, x1= 2, maxiter = 5 and xtol = 1e-4
cos(2x).x³; with x0=1, x1= 2, maxiter = 15 and xtol = 1e-8
cos(2x).x³ with x0=1, x1= 2, maxiter = 3 and xtol = 1e-8

c) Write a function defined as: def GaussSeidel(Aaug, x, Niter = 15):

Purpose: use the Gauss-Seidel method to estimate the solution to a set of N linear equations expressed in matrix form as Ax = b. Both A and b are contained in the function argument - Aaug.

Aaug: an augmented matrix containing [A | b ] having N rows and N+1 columns, where N is the number of equations in the set.
x: a vector (array) contain the values of the initial guess
Niter: the number of iterations (new x vectors) to compute
return value: the final new x vector.

Write and call a main() function that uses your GaussSeidel function to estimate and print the solutions to the following sets of linear equations:

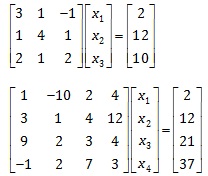
d) Write a function defined as: def Inverse(A):
Purpose of Inverse(A): use the Gauss-Jordan Elimination*to find the inverse of the A matrix.

A: is a square matrix of n-rows by n-cols.
return value: A-1 is the inverse of matrix A

Write and call a main() function that uses your Inverse function to calculate and print the solution A-1 matrix for the A matrices of part c). Also, verify that A-1 is in fact the inverse of A by performing the operation A-1A and obtaining the proper identity matrix. Use the inverse matricies to solve the equations in part c) and output the result to the console. Output statements should be informative and nicely formatted.

*note: you may use my code Gauss_Elim.py as a starting point for part d.

Attachment:- Computer Methods in Analysis and Design.rar