Reference no: EM131126349
1. Solve the following equation. Determine whether the equation is an identity, conditional equation, or an inconsistent equation: 3-5(2x+1)-2(x-4)=0
a. 1/4, identity
b. 1/6, inconsistent
c. 1/9, conditional
d. 1/2, conditional
2. Find the slope of the line passing through each pair of points or state that the slope is undefined: (0, a) and (b, 0)
a. M=-a/b
b. Undefined
c. M=a/b
d. M=-a/ab
3. Find the slope of the line passing through each pair of points or state that the slope is undefined: (a, b) and (a, b + c)
a. =-b/abc
b. =b/ab
c. Undefined Slope
d. =a/abc
4. Find all the zeros of each polynomial function and write the polynomial as a product of linear factors.
f(x) = 2x4 + 3x3 + 3x - 2
a. -2, 1/2, +- i ; f(x) = (x - i)(x + i)(x + 2)(2x - 1)
b. 2, 1/2, +- i ; f(x) = (x - i)(x - i)(x + 2)(2x - 1)
c. -2, 1/2, +- i ; f(x) = (x + i)(x + i)(x + 2)(2x - 1)
d. -1, 1/2, +- i ; f(x) = (x - i)(x + i)(x + 2)(2x + 1)
5. e5x-3 - 2 Solve the following exponential equation. Express the solution set in terms of natural logarithms or common logarithms to a decimal approximation, of two decimal places, for the solution:
a. {ln 10, 478 + 3/5}; ˜ 2.45
b. {ln 10, 376 + 3/5}; ˜ 1.78
c. {ln 12, 402 + 2/5}; ˜ 2.16
d. {ln 10, 277 + 3/8}; ˜ 1.57
6.
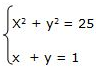Solve the following system:
a. {(2, -3), (-1, 4)}
b. {(4, -8), (-2, 4)}
c. {(1, -2), (-2, 9)}
d. {(4, -3), (-3, 4)}
7. Solve the following system of equations using matrices: x + 2y - z = -3 2x - 4y + z = -7 -
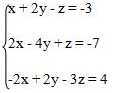
2x + 2y - 3z = 4
a. {(-4, 1/2, 0)}
b. {(-3, 1/2, 1)}
c. {(-2, 1/2, -1)}
d. {(3, 1/2, 2)}
8. Locate the foci and find the equations of the asymptotes. (y+2)2/4 - (x-1)2/16 = 1
a. foci: (1, -1+-2v4); asymptotes: (y + 2) = 1/2 (x - 2)
b. foci: (1, -2+-2v3); asymptotes: (y + 2) = 1/2 (x - 2)
c. foci: (1, -2+-2v5); asymptotes: (y + 2) = 1/2 (x - 1)
d. foci: (1, -2+-2v7); asymptotes: (y + 2) = 1/2 (x - 2)
9. Locate the foci and find the equations of the asymptotes: (x - 1)2- (y - 2)2 = 3
a. foci: (1 {16, 2); asymptotes: (y - 2) = {(x - 1)
b. foci: (1 {12, 2); asymptotes: (y - 3) = {(x - 3)
c. foci: (1 {12, 2); asymptotes: (y - 1) = {(x - 1)
d. foci: (1 {14, 2); asymptotes: (y - 2) = {(x - 1)
10. In a class of 50 students, 29 are Democrats, 11 are business majors, and 5 of the business majors are Democrats. If one student is randomly selected from the class, find the probability of choosing: (a) Democrat who is not a business major. (b) A student who is neither a Democrat nor a business major.
a. a. 11/25 b. 4/10
b. a. 12/25 b. 3/10
c. a. 9/25 b. 6/10
d. a. 7/25 b. 5/10