Reference no: EM132363839

SGTA Exercises - Quantifiers, Graph Theory

Q1. 'To use the wireless network at the airport you must pay a daily fee unless you are an employee of the airport'. Define three relevant propositions w, d and e, and write the sentence using propositional logic.

Q2. Translate these system specifications into English where the propositional function S(x, y) is 'x is in state y '. The domain for x is all systems, and the domain for y is all possible states.

(a) ∃x S (x,'open')

(b) ∀x (S(x,'malfunctioning') ∨S(x,'diagnostic'))

(c) (∃x S (x,'open')) ∨ (∃x S (x,'diagnostic'))

Q3. Convince yourself that (p ∧ q) → r and p → (q → r) are logically equivalent. Write your argument clearly, but precisely.

Definition: A subgraph of a graph G is a graph obtained from G by deleting some edges and/or some vertices and all their incident edges.

4. Determine whether the following statements are true or false for simple graphs G = (V, E), where V denotes the set of vertices and E is the set of edges.

Give a short proof of each true statement and give a counter-example for each false statement. Identify which of these change truth value if G is allowed to be a multi-graph or pseudo-graph.

(a) A (simple) graph with |E | ≥ |V | is connected.

(b) A (simple) graph with |E | ≥ |V | contains a cycle.

(c) A (simple) graph with |E | ≤ |V | -2 is not connected.

(d) A (simple) graph with |E | ≥ |V | -2 is acyclic (i.e., has no cycles).

(e) A (simple) graph with 2 components has at most |V | -2 edges.

(f) A (simple) graph with |E | = |V | -2 has at least 2 components.

(g) A (simple) graph with |E | = |V | -2 has exactly 2 components.

(h) If G is a connected (simple) graph containing a cycle, then the removal of any edge of the graph leaves the graph connected.

Q5. Translate the following logical constructions into natural plain English, where F (p) is 'Printer p is out of service', B (p) is 'Printer p is busy', Q(j ) means 'Print job j is queued', and L(j ) means 'Print job j has been lost'.

(a) ∃p (F (p) ∧B (p)) → ∃j L (j)

(b) ∀p B (p) → (∃j Q (j))

Q6. Negate the following predicates (= propositional function).

(Shift '¬' as far inside the predicate as possible.)

Comment on the truth or falsity of the predicate and its negation.

(a) ∀x ((x ≥ 100)∨ (x < 100))

(b) ∃y ∀x ((y > 0) ∧ (x < y))

(c) ∀x ∃y (¬M (x,y) → ¬N (x,y))

Q7. In one of last week's lectures, we saw the NAND connective, p ↑ q. We saw that ¬p is equivalent to p ↑ p , and p ∧ q is logically equivalent to (p ↑ q) ↑ (p ↑ q) - since by definition p ↑ q = ¬(p ∧ q).

Show that p ∨ q can be written solely in terms of NAND operations.

Q8. Formulate the following sentence into a logical proposition. Is it true?

'The number 100 can be written as the sum of 2 squares.'

Q9. Determine whether a (simple or non-simple) graph having five vertices can exist, such that the degrees of the vertices are given as follows. If so, draw such a graph. If not, explain why it cannot exist.

(a) {2,3,3,3,3} (b) {2,2,3,3,4}

Q10. Show that a simple graph G having 6 vertices and 14 edges must contain a sub-graph isomorphic to K₅, and hence cannot be planar. Describe G as a sub-graph of K_n for the minimal value of n. Be precise in describing what needs to be deleted from K_n to get G.

Q11. A simple graph has 33 edges, and every vertex has degree 7 or 8. How many vertices does the graph have? Describe this graph as a sub-graph of K_n for some integer n, obtained by deleting some vertices and/or edges. What is the minimum value for n and what needs to be deleted?

Be precise in describing what needs to be deleted.

Q12. Decide whether G₁ and G₂ are equivalent, where G₁ has vertices {1, 2, 3, 4, 5, 6, 7, 8} and edges {12^-, 17^-, 18^-, 23^-, 28^-, 34^-, 35^-, 45^-, 46^-, 56^-, 67^-, 78^-} while G₂ has vertices {a, b, c, d, e, f, g, h} and edges {ab^-, ae^-, ah^-, bc^-, bh^-, cd^-, cg^-, de^-, df^-, ef^-, fg^-, gh^-} .

(Here 18means there is an edge joining vertex 1 to vertex 8.) HINT: draw the graphs, then draw conclusions.

Q13. If P is a path in a weighted graph from vertex A to vertex B, we call the total weight of the edges in P the distance along P from A to B. Recall that the length of a path is the number of edges in the path. The following questions refer to the weighted graph at right.

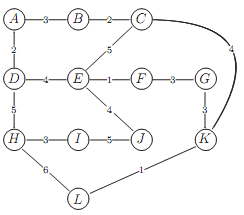
(a) List the vertices that can be reached from vertex A with a path of length 1 and determine the total weight of each of those paths.

(b) List the vertices that can be reached from vertex A with a path of length at most 2 and determine the minimum distance from A to these vertices if you restrict yourself to paths of length at most 2.

(c) List the vertices that can be reached from vertex A with a path of length at most 3 and determine the minimum distance from A to these vertices if you restrict yourself to path of length at most 3.

(d) Hence, or otherwise, find the minimum distance from A to G along any path.

Q14. Addition of Real numbers is associative; which is to say that a + (b +c) = (a +b) + c for all a, b, c ∈ R. Is implication associative? That is, is (p → q) → r logically equivalent to p → (q → r), for every possible p, q, r?

Q15. Formulate the following sentence into a logical proposition.

'Every positive integer can be written as the sum of 2 squares.'

Q16. Taking n to be an integer, is '¬∃n (10 = 8n)' true or false?

Q17. Let G be a simple graph with v vertices and e edges.

Let m be the minimum of the degrees of the vertices of G.

Explain why 2e/v ≥ m.

Q18. A particular planar graph has 7 vertices - 6 of degree 3 and one of degree 6.

• How many edges does it have?
• How many faces has it when drawn on the sphere? (or, regions when drawn in the plane)
• Draw a graph consistent with this information.

Q19. Explain why a simple graph with n vertices must be connected if the number of edges is at least ½(n -1)². [Hint: If it is not connected, what can you say about the maximum degree of any vertex?]