Reference no: EM131970632

Assignment - Need to solve only questions 1 (c), 2 (c), 3 (a, b), 4 (a, b), 5 (a, b), 6 (b), 7 (b), 8 (b) and 9 (a)

Asymptotic Complexity -

Given two functions f, g : R⁺ |→ R,

1. f ∈ O(g(n)) if and only if ∃ c ∈ R⁺, n₀ ∈ R^≥0 (∀n ≥ n₀ (f(n) ≤ c · g(n))).

2. f ∈ Ω (g(n)) if and only if ∃ c ∈ R⁺, n₀ ∈ R^≥0 (∀n ≥ n₀ (f(n) ≤ c · g(n))).

3. f ∈ Θ (g(n)) if and only if O(g(n)) and Ω(g(n)).

1. Give derivations that prove the following. For convenience, you may assume that the logarithms are in the base of your choice, but you should specify what base you are using in your derivation.

(a) (n - 8)² ∈ Θ(n²).

(b) 7n⁴ - 5n³ log n - 6n² + 9n log n - 13n ∈ ?(n⁴).

(c) 2 log(3n³ - n² + 43) ∈ O(log n).

2. Prove that each of the following are false (using the definitions of O and Θ).

(a) 3n^7/2 - 2n² is O(n³log n).

(b) n³/58 - 7n² log n is Θ(n²).

(c) 4ⁿ ∈ O(2ⁿ).

3. In this question, you will prove that

log(n!) = Θ(n log n).

Recall that n! = n x (n - 1) x · · · x 2 x 1.

(a) Show that log(n!) ∈ O(n log n). [Hint: log(a x b) = log a + log b.]

(b) Show that log(n!) ∈ ?(n log n). [Hint: Consider only the first n/2 terms.]

4. You are given an algorithm that uses T(n) = a · n² + b · 3ⁿ basic operations to solve a problem of size n, where a and b are some real non-negative constants.

Suppose that your machine can perform 400,000,000 basic operations per second.

(a) If a = b = 1, how long does it take for your algorithm to solve problems of size n = 10, 20, 50.

For each size of n, include the time in seconds and also using a more appropriate unit (minutes, hours, days, years, centuries, or millennia! Assume that a year is 365 days.).

(b) Let a = 0 and b = 1/9. Find the largest value of n that that allows the algorithm to run in less than a year.

5. Suppose that Algorithm A has runtime complexity O(n³) and Algorithm B has runtime complexity O(n log n), where both algorithms solve the same problem.

(a) How do the algorithms compare when n = 12?

(b) How do the algorithms compare when n is very large?

Induction

6. For this question, you are not allowed to use the known solution of what the sum of a geometric sequence is.

(a) Consider the inequality, for all n ≥ 2, given by

_i=1∑ⁿ4/5ⁱ < 1

Why would it be difficult to prove this using induction?

(b) In order to prove the inequality in (a), prove the following stronger inequality, for all n ≥ 2, using induction instead. Show why proving this bound proves (a).

_i=1∑ⁿ 4/5ⁱ ≤ 1 - 1/5ⁿ

7. Consider the Fibonacci numbers:

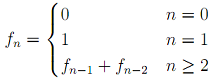
(a) Prove by induction that fn ≥ (1.5)^n-1, for all n ≥ l_a. Find the smallest positive integer l_a you can for this.

(b) Prove by induction that f_n ≤ ((1+√5)/2)^n-1, for all n ≥ l_b. Find the smallest positive integer l_b you can for this.

8. Consider the following recursive definition:

(a) List the first 5 elements in the sequence {a_n}.

(b) Prove by induction that a_n = 2n² - 3n + 5 for n ≥ 1.

9. This question is about tiling shapes with L-trominoes: three 1 x 1 squares attached so that they form an L-shape. To tile a shape means to fill it completely with non-overlapping copies of a base shape. For example, Figure 1 shows that we can tile an 8 x 8 square whose top-left corner is missing with L-trominoes.

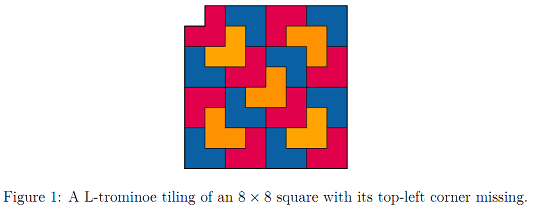
(a) Prove that for n ≥ 1, any 2ⁿ x 2ⁿ square with one corner missing can be tiled with L-trominoes.

Extra Problems -

10. Consider the following algorithm:

for i from 1 to n do

for j from A to B do

print 'q'

end do

end do

(a) How many times is q printed when A = 10 and B = 23?

(b) How many times is q printed when A = n - i and B = n?

(c) How many times is q printed when A = 1 and B = n - 1?

(d) How many times is q printed when A = i and B = n - 1?

(e) How many times is q printed when A = 1 and B = n²?

11. The n-th harmonic number, denoted H_n, is defined by the sum

H_n = 1 + 1/2 + 1/3 + 1/4 + · · · + 1/n = _k=1∑ⁿ 1/k.

In this question, you will prove that H_n ∈ Θ(log n).

(a) Show that H_n ∈ Θ(log n). [Hint: First look at the last n/2 terms.]

(b) Show that H_n ∈ ?(log n).

12. (a) Prove by induction that 1 + 2ⁿ ≤ 3ⁿ for all n ≥ 1.

(b) Prove by induction, for all n ≥ 1, that

_i=1∑ⁿ 1/(i(i + 1)) = n/(n+1)

More Extra Questions -

13. Let a and b be real numbers. Prove that min(a, b) x max(a, b) = a x b.

14. The absolute value of a real number x, denoted |x|, is defined as

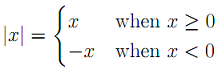
Note that if a = |b|, then a = ±b.

(a) The triangle inequality states that for all real numbers x and y,

|x + y| ≤ |x| + |y|.

Prove this result.

(b) Let x and y be integers that are not equal. Prove that there is a unique real number z such that |x - z| = |y - z|.

(c) From part (b), was it necessary that x ≠ y for your proof to work?