Reference no: EM13838485
Problem 1: Consider the following linear programming problem:
Max 3A + 3B
s.t.
2A + 4B ≤ 12
6A + 4B ≤ 24
A, B ≥ 0
a. Find the optimal solution using the graphical solution procedure.
b. If the objective function is changed to 2A + 6B, what is the optimal solution?
c. How many extreme points are there? What are the values of A and B at ach extreme point?
Problem 2: Given the linear program
Max 3A + 4B
s.t.
-1A + 2B ≤ 8
1A + 2B ≤ 12
2A + 1B ≤ 16
A, B ≥ 0
a. Write the problem in standard form.
b. Solve the problem using the graphical solution procedure.
c. What are the values of the three slack variables at the optimal solution?
Problem 3: Consider the following linear program:
Max 2A + 3B
s.t.
5A + 5B ≤ 400 Constraint 1
-1A + 1B ≤ 10 Constraint 2
1A + 3B ≥ 90 Constraint 3
A, B ≥ 0
Figure 1 shows a graph of the constraint lines.
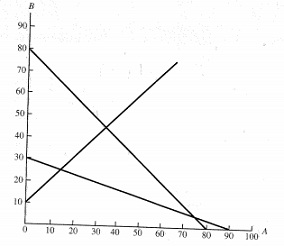
a. Place a number (1, 2, or 3) next to each constraint line to identify which constraint it represents.
b. Shade in the feasible region on the graph.
c. Identify the optimal extreme point. What is the optimal solution?
d. Which constraints arte binding? Explain.
e. How much slack or surplus is associated with the nonbinding constraint?
Problem 4: Consider the following linear programming problems:
Min A+ 2B
s.t.
A + 4B ≤ 21
2A + B ≥ 7
3A + 1.5B ≤ 21
-2A + 6B ≥ 0
A, B ≥ 0
a. Find the optimal solution using the graphical solution procedure and the value of the objective function.
b. Determine the amount of slack or surplus for each constraint.
c. Suppose the objective function is changed to max 5A + 2B. find the optimal solution and the value of the objective function.
Problem 5: Consider the following linear program:
Max 1A - 2B
s.t.
-4A + 3B ≤ 3
1A - 1B ≤ 3
A, B ≥ 0
a. Graph the feasible region for the problem.
b. Is the feasible region unbounded? Explain.
c. Find the optimal solution.
d. Does an unbounded feasible region imply that the optimal solution to the linear program will be unbounded?