Reference no: EM131083962
Math 176: Algebraic Geometry, Fall 2014- Assignment 3
1. Decompose each of the following algebraic sets into irreducible components. Justify that each of your irreducible component is indeed irreducible.
(a) V(y4 - x2, y4 - x2y2 + xy2 - x3) ⊂ A2(C).
(b) V(x2 - yz, xz - x) ⊂ A3().
2 Let I = (x2 - y3, y2 - z3) ⊂ C[x, y, z]. In this problem we will prove V(I) is a variety.
(a) Show that every element of C[x, y, z]/I can be represented as a + xb + yc + xyd for some polynomials a, b, c, d ∈ C[z].
(b) Define φ : C[x, y, z] → C[t] by φ(x) = t9, φ(y) = t6, φ(z) = t4.
If f = a + xb + yc + xyd for some a, b, c, d ∈ C[z], and φ(f) = 0, conclude f = 0.
(c) Deduce that ker(φ) = I and V(I) is irreducible.
3. Let f ∈ k[x1, . . . , xn] and let V = V(f). Suppose V is a variety. Prove there is no variety W with V 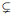 W
W 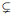 An.
An.
4. Let V, W ⊂ An be algebraic sets and suppose V ⊂ W. Show that each irreducible component of V is contained in some irreducible component of W.
5. Prove that there are three points P1, P2, P3 ∈ A2(C) such that, rad(I) = mP1 ∩ mP2 ∩ mP3, where I = (x2 - 2xy4 + y8, y3 - y) and mPi = I({Pi}).
|
Examine the spectrum of the signal x(n)
: examine the spectrum of the signal x(n).
|
|
Probability that the plane will complete
: What is the probability that the plane will complete its next flight safely?
|
|
Defective item with probability
: Suppose that a machine produces a defective item with probability p and produces a non-defective item with probability 1 - p.
|
|
Independent uniform random variables
: X1,..., Xn are independent uniform random variables, all with expected value µX = 7 and variance Var[X] = 3. (a) What is the PDF of X1?
|
|
Justify irreducible component is indeed irreducible
: Math 176: Algebraic Geometry, Fall 2014- Assignment 3. Decompose each of the following algebraic sets into irreducible components. Justify that each of your irreducible component is indeed irreducible. V(y4 - x2, y4 - x2y2 + xy2 - x3) ⊂ A2(C)
|
|
Problem regarding the normal density curve
: Find endpoint(s) on the given normal density curve with the given property: Explain how you got your answer please. (a) The area to the right of the endpoint on a N(50, 4.7) curve is about 0.01. What is the endpoint?
|
|
Determine the number of complex multiplications
: determine the number of complex multiplications.
|
|
Calculate the test statistic correct
: 1. State the direction of the alternative hypothesis used to test the state office's belief. Type gt (greater than), ge (greater than or equal to), lt (less than), le (less than or equal to) or ne (not equal to) as appropriate in the box. 2. Use t..
|
|
An iid sequence of exponential random variables
: X1,..., Xn is an iid sequence of exponential random variables, each with expected value 5. (a) What is Var[M9(X)], the variance of the sample mean based on nine trials?
|