Justify by finding the expressions for work done

Reference no: EM13810016

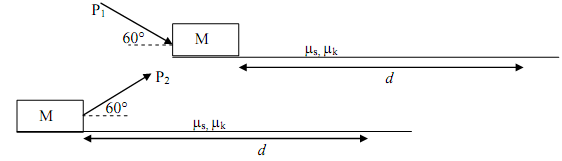
1) Jack and Jill are assigned the task of mowing Joe's yard. To add to their woes, the mowers given to them are identical, heavy, unmotorized and old-fashioned. Both are lazy and want to do minimum work (i.e. mechanical work) while mowing. Jack pushes the mower with minimum force P1 (as shown) while Jill pulls her mower with miniumum force P2. Both mowers are initially at rest. The ground obviously is rough (µs, µk).

Both mow till distance 'd'.

- Who did more (mechanical) work: Jack or Jill? Why? Justify by finding the expressions for work done by both Jack and Jill.

- Having covered a distance 'd', whose mower is moving faster: Jack's or Jill's? Justify by finding the expressions for final speeds of Jack and Jill's mowers.

2341_Expressions for work done.png

2) A linear Hooke's spring has an unstretched length of 30 cm and a stiffness of 20 N/m. The spring is pivoted/fixed at point G (as shown) and is massless. A force P is applied to compress the spring from its initial position H to the pivot/fixed point G. Assume the spring follows the shape of the rods (as shown) at every instant. The force P is constant in magnitude and always tangential (during motion) to the rod/spring in each case. Neglect friction.

a) For which case the spring will store the most potential energy at G?

b) For which case the spring will store the most potential energy at H?

c) For which case the force P (needed to compress the spring to point G) will be the largest?

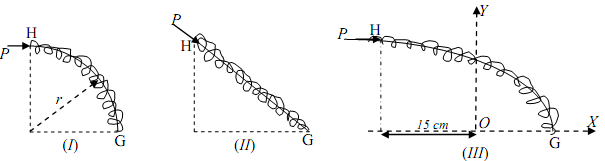
2255_Expressions for work done1.png

CASE I: Circular rod with radius, r = 14 cm
CASE II: Straight rod; length HG = 20 cm
CASE III: Parabolic rod, y² = (4-x), where x, y are in cm w.r.t the XY system at O.

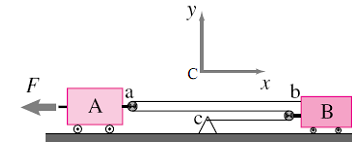
3) The two masses shown in figure have round frictionless massless pulleys. The inextensible cord connecting them is always taut. Given that F = 130 N; mA = mB = 30 kg, find the acceleration of the two blocks and tension in the cable when the system is released/pulled from rest. The floor is rough with µs = 0.2 and µk = 0.1.

192_Expressions for work done2.png

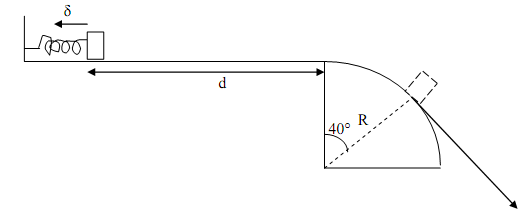
4) What initial deformation (compression), δ, in the spring will make the mass leave the circular ramp at 40° (as shown)? The path is entirely frictionless. The mass initially starts off from rest. Note the mass and the spring are not rigidly attached to each other. (m = 1 kg, k = 200 N/m, R = 25 cm, d = 1 m, g = 10 m/s²)

694_Expressions for work done3.png

Reference no: EM13810016

Questions Cloud

Different types of total quality management : There are different types of total quality management (TQM) tools that can be used in quality management. These tools are useful in analyzing data and determining the methods of improving the quality process for an organization.

Differential psychology focus on identifying : What five physical areas between people does differential psychology focus on identifying? Is it important for managers to understand their employees' differences? Why or why not? Explain your viewpoint by giving a minimum of two specific examples..

Penetration testing proposal using specific pen-testing tool : Write a 3-5 page penetration testing proposal using specific Pen-testing tools and based on a DoS scenario

Organizational development process skills : Apply the best organizational development process skills the executives should use. Apply the change strategies within the short-term and long-term

Justify by finding the expressions for work done : Having covered a distance 'd', whose mower is moving faster: Jack's or Jill's? Justify by finding the expressions for final speeds of Jack and Jill's mowers - Justify by finding the expressions for work done by both Jack and Jill.

The sarbanes-oxley act is intended to increase confidence : The Sarbanes-Oxley Act is intended to increase the confidence of the public and investors through increasing which of the following

Situation and present the argument : It should be one page, word processed and double-spaced. It should be well analyze the situation and present the argument.

Calculate the control limits : Calculate the control limits for the X-bar and s chart for assembly line 1. Calculate the control limits for the X-bar and R chart for assembly line 2.

Why globalization is good or not good for a business : Write an argumentative paper of no more than 750 words that demonstrates why globalization is good or not good for a business. The paper should define the term good, and should identify the premises and conclusions.

User Account

All Pages