ITECH1400 Foundations of Programming Assignment

Assignment Help Programming Languages

Reference no: EM132526992

ITECH1400 Foundations of Programming - Federation University

Logarithms, Benford's Law and Fraudulent Data

Overview
In this assignment you will write an application in Python that will apply Benford's Law to a given set of your own data. This is an individual assignment.

Learning Outcome 1: Recall and use typical programming constructs to design and implement simple software solutions.

Learning Outcome 2: Reproduce and adapt commonly used basic algorithms.

Learning Outcome 3: Explain the importance of programming style concepts (documentation, mnemonic names, indentation)

Learning Outcome 4: Write and implement a solution algorithm using basic programming constructs. S3. Demonstrate debugging and testing skills whilst writing code.

Learning Outcome 5: Develop self-reliance and judgement in adapting algorithms to diverse contexts.

Learning Outcome 6: Design and write program solutions to identified problems using accepted design constructs.

Assessment Task

Develop a Python program which will load up a set of data, determine the frequencies of the leading digits and compare them with the predicted distribution of Benford's law. Display this in a bar chart and a table of values. For example:

Digit 1: Observed = 0.321 Expected = 0.301
Digit 2: Observed = 0.153 Expected = 0.176 and so on up till digit 9.

We shall look at three cases.

An Excel spreadsheet has been taken from Office-Watch: Benford's Law and Excel5 to let you quickly visualize the Python application that we need make.

Case 1 - Fibonacci series
This series begins with two numbers 1,1 - these two numbers are added to continue the series giving rise to the following (only the first 8 terms of the series are shown here):

1,1,2,3,5,8,13,21,. . .

There are many examples of this pattern in Nature and the series is closely related to the Golden7 ratio.

Using the Excel spreadsheet generate a Fibonacci series up to the 24th term and see if the first digits obey Benford's Law. Does it get better if you add more terms?

The Chi-test8 measures how close an actual value is to the expected value - the closer it is to 100% the closer the actual value is to the expected value. In our case, we are testing how close the frequency of each digit in our dataset is to Benford's prediction for that digit.

What is the value of the ChiTest comparison for this Fibonacci series? Does it get better if we add more terms to the series?

Case 2 - Fibonacci numbers & Benford's law using Python

In this case you are to repeat the analysis in Case 1 but using you Python code.

Case 3 - Length of Rivers in the World

In this case, use your Python code to see whether the lengths of rivers in the world follow Benford's law.

Fraud detection using Benford's Law

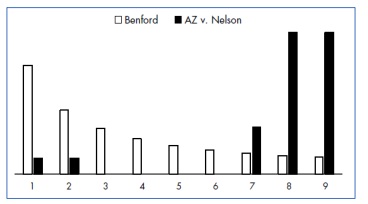
One use of Benford's Law is to detect cases of Fraud. Consider the 1993 case of State of Arizona v Nelson. The accused diverted nearly $2M to fake vendors in an attempt to defraud the State. The frequency of first digits in the written cheques clearly violates Benford's Law leading to a conviction.

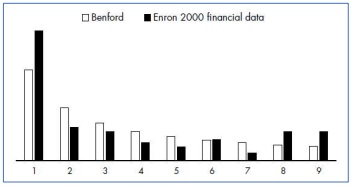
Another case is that of Enron in its posting of revenue for the year 2000. Comparison of the frequency of first digits versus the expected frequency shows large discrepancies. The company went bankrupt the following year - one of the greatest financial failures in history.

Attachment:- Foundations of Programming.rar

Reference no: EM132526992

Questions Cloud

Logarithms - benfords law and fraudulent data assignment : Logarithms, Benford's Law and Fraudulent Data Assignment Help and Solution - Recall and use typical programming constructs

Explain the incompetency of the health care professional : In this module, you learned about the medical education system and requirements of licensing. As you can imagine, the competency of medical professionals.

What are three purposes of budgeting : How does the management by exception concept relate to budgeting? What are five basic principles which, if followed, should improve the probability

How would scotti report september sale of treasury shares : How would Scotti report the September 15th sale of the treasury shares? On January 1, 2018, its first year of business, Scotti Company issued 800,000 shares.

ITECH1400 Foundations of Programming Assignment : ITECH1400 Foundations of Programming Assignment Help and Solution, Federation University - Assessment Writing Service - Logarithms, Benford's Law and Fraudulent

How ferguson and son company budgetary control system : Explain how Ferguson & Son Manufacturing Company's budgetary control system could be revised to improve its effectiveness.

Research and report on current or recent malware : Research and report on a current or recent malware (e.g., Trojan, virus, or worm) attack. Describe its method and effects.

What is the ph at the equivalence point in the titration : 1. What is the pH at the equivalence point in the titration of 100 mL of 0.10 M HCl with 0.10 M NaOH?

How time is conceived for different cultural groups : Explain how time is conceived for different cultural groups. Pick a cultural group and explain in your own words. The response must be typed.

User Account

All Pages