Reference no: EM13834334

Problem 1: Use the definition of an improper integral to evaluate the integral below:

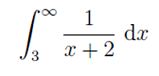
Problem 2: Determine whether the improper integral is convergent or divergent. Do not evaluate the integral.

(a). The volume obtained when the area between the positive x-axis (x > 0) and the graph of f(x) = 1/e^x is revolved about the x-axis

(b). The volume obtained when the area between the positive x-axis (x > 0) and the graph of f(x) = 1/ex is revolved about the y-axis.

Problem 3: Find the indefinite integral and evaluate the definite integral:

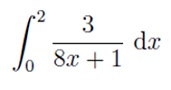
Problem 4: Evaluate the integral as a sum of two integrals:

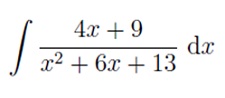
Problem 5: Evaluate:

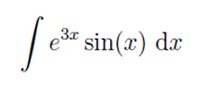
Problem 6: (a) Suppose we divide the integral (1, 4) into 100 equally wide subintervals and calculate a Riemann sun for f(x) = 1 + x² by randomly selecting a point c_i in each subinterval. We can be certain that the value of the Riemann sum is within what distance of the exact value of the area between the graph of f and the interval (1, 4)?

(b) What if we take 200 equally long subintervals?

Problem 7: Sketch the graph of the integrand function and use it to help evaluate the integral

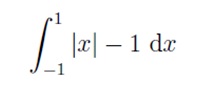
Problem 8: (a) Find the area between f(x) = 1/x and the x-axis for 1 < x < 10, 1 < 100, and 1 < x < A. What is the limit of the area for 1 < x < A as A → ∞?

(b) Find the volume swept out when the region in part (a) is revolved about the x-axis for 1 < x < 10, 1 < x < 100, and 1 < x < A. What is the limit of the volumes for 1 < x < A as A → ∞?

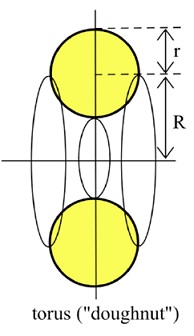
Problem 9: The center of a circle in the figure below with radius r is at the point (0, R). Use the Theorems of Pappus to find the volume and surface area swept out when the circular region is rotated about the x-axis.

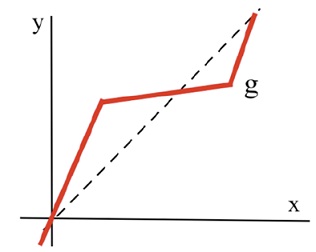
Problem 10: The figure below shows the graph of g. sketch the graph of g^-1.  

Problem 11: Find the exact values of:

(a) tan(cos^-1(x))

(b) cos(tan^-1(x))

(c) sec(sin^-2(x))

Problem 12: Use the definition of an improper integral to evaluate the given integral:

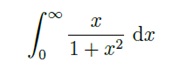
Problem 13: Determine whether the improper integral is convergent of divergent. Do not evaluate the integral:

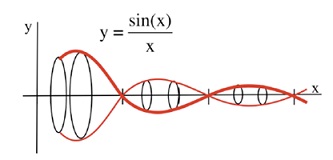
The volume obtained when the area between the x-axis for x > 1 and the graph of f(x) = sin(x)/x (in the figure below) is revolved about the x-axis,

Problem 14: Complete the square in the denominator, make the appropriate substitution, and integrate:

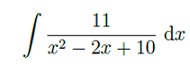
Problem 15: Use the tube method to calculate the volume when the region between the x-axis and the graph of y = sin(x) for 0 < x < π is rotated about the y-axis.

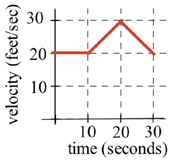
Problem 16: A car had the velocity given in the figure below. How far did the car travel from t=0 to t=30 seconds?