Implement the priorityq class using a heap instead

Assignment Help Data Structure & Algorithms

Reference no: EM13811196

Part I: Written exercises.

1. Using the Red-Black Tree applet, you input the following numbers into the Red-Black tree, keep all red-black rules ( see the red-black rule on the bottom of the exercise ) either using color changes or rotation. The result graph should be height balance and red-black correct.

You need to follow the rules, randomly color change and rotation will result in zero credit even the result could be red-black correct.

Attach your results of screen shots for every question.

a. Insert 50, 70, 20, 90

b. Insert 50, 70, 20, 90, 99

c. Insert 50, 70, 20, 90, 80

d. Insert 50, 70, 20, 80, 60, 90, 75, 95

e. Insert 50, 70, 20, 90, 60, 55, 65, 68

Red-Black Rules

When inserting (or deleting) a new node, certain rules, which we call the red-black rules, must be followed. If they're followed, the tree will be balanced. Let's look briefly at these rules:

1. Every node is either red or black.
2. The root is always black.
3. If a node is red, its children must be black (although the converse isn't necessarily true).
4. Every path from the root to a leaf, or to a null child, must contain the same number of black nodes.

2. Given input {4371, 1323, 6173, 4199, 4344, 9679, 1989} and a hash function h(x) = x %10 (table size is 10), showing the resulting

a. Separate chaining hash table
b. Open addressing hash table using linear probing.
c. Open addressing hash table using quadratic probing.
d. Open addressing hash table with second hash function h2(x) = 7- (x %7)

3. Draw the figures to show steps how to convert the binary tree to a heap using the Heapify algorithm.

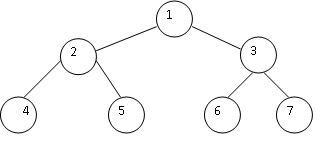
4. Using the diagrams (see the attached example of heap sort) to trace the action of heapsort on the list of 1, 7, 2, 6, 3, 5, 4, give every state of your tree such as finishing a heapify or removing the root.

Part II: programming exercise

Implement the PriorityQ class using a heap instead of an array.

Attachment:- heat short.pdf

Reference no: EM13811196

Questions Cloud

Write the nuclear equation for decay : Write the nuclear equation for decay - Calculate the binding energy per nucleon and How many nuclei are initial present in a 25.0 mg sample?

Complete development of a relational database : Complete development of a relational database. You are to do the following: Use Visio to create the appropriate diagrams. Create a script named mdbXXX.sql (where XXX are your initials) that Create the tables in 3NF needed to implement your DB schema

Examine the relationship between negotiation : The purpose of this assignment is to examine the relationship between negotiation, ethics, and effective leadership.

Schedule a meeting with a vendor who lives there : While working in Somalia, you schedule a meeting with a vendor who lives there. When he shows up 20 minutes after the meeting was scheduled, should you take it as a sign of incompetence or disrespect? Explain your answer using concepts from the te..

Implement the priorityq class using a heap instead : Implement the PriorityQ class using a heap instead of an array

Qualified national or international standards body : What is the certification when a qualified national or international standards body or similar certifying agency audits and certifies that a company is ISO 9000-compliant?

Essential features of a project plan : Which project progress technique includes the essential features of a project plan, budgeted cost of work scheduled and budgeted cost of work performed?

Perpetual system for inventory management : 1. Which of the following is an input file necessary to run an MRP program? 2. Which of the following is a perpetual system for inventory management?

Self-service approach to service design : What happens to production efficiency as the customer exerts more influence on the system? Why do many customers like the self-service approach to service design?

User Account

All Pages