Reference no: EM133302077

Part 1:

Assignment 1

Consider the data set D = {(x_n, t_n)}^N_n=1, where the ordered pairs are formed by feature vectors x_n ∈ R^d and labels t_n ∈ {-1, +1}. By Bayes Theorem we have that the posterior probability P(t|x) for the class t is given by:

P(t|x) = P(x|t)P(t)/P(x| - 1)P(-1) + P(x| + 1)P(+1)

where the priors P(t) satisfy that P(-1) + P(+1) = 1. If we model the distri- bution of features inside class t by a Gaussian distribution with mean µt and covariance matrix Σ_t,demonstrate that:

1. The function σ : R^d → {-1, 0, 1} defined as:

σ(x) = sgn(log P(x| + 1) - log P(x| - 1) + log P(+1)/1-P(+1) where sgn(x) = 1 if x > 0, -1 if x < 0, and 0 otherwise, is a discriminant function.

2. The boundary of classification is a determined by a quadratic form.

covariance matrix, i.e. Σ₊₁ = Σ_-1 = Σ then the boundary of classification. If the dispersion of points inside each class can be described by the same tion is given by the linear equation

0 = w^Tx + w₀,

where

w = Σ^-1(µ₊₁ - µ_-1)

w₀ = -1/2 [µ^T₊₁Σ^-1µ₊₁

- µ^T_-1Σ^-1µ_-1] + log P(+1)/1-P(+1).

Hint: The multivariate Gaussian centered at µt with covariance Σt is given by the expression:

P(x|t) = 1/(2Π)^d/2√det(Σ) exp {-1/2(x-u_t)^TΣ^-1(x - µt)}

Assignment 2

Four temperature censors were tted in the four corners of a room. Each of them take a temperature reading every 30 minutes. There is a door in the front of the room, that we suspect was opened at some point during the measurement. Your task is to determine, by using PCA and K -means, whether the door was open or not. The measurements were stored in the le 'room-temperature.csv'. Each line of the le is composed by ve entries, a time-stamp and readings from four sensors: front-left reading, front-right reading, back-left reading, and back-right reading.

1. Load the le 'room-temperature.csv' and plot the readings against time (do not use the time-stamp, use the order index as time variable).

2. Proceed to the PCA analysis keeping the components responsible for 93% of the variance. Plot these two components against time.

3. Plot the readings of the back-left sensor against the fron-left sensor and the readings of the back-right sensor against the front-right sensor. Discuss your observations.

4. Perform a K-means test for k = 2, 3, 4, 5 and, by using a suitable criterion, decide which k better represents the data.

5. Did somebody open the door during the measurement? Why?

Assignment 3

Question 1. Show that for the polynomial kernel function K : R² × R² → R defined as

K(x, y) = (x^Ty + 1)²

can be expressed as

K(x, y) = φ(x)^Tφ(y),

where φ : R² → R⁶ is defined by:

φ(x) =

Question 2. Consider the le 'support.csv'. In each of its 3000 rows you may nd the coordinates of a point in R2 and its classi cation (+1 or -1). Plot the points on a scatter graph and decide whether the problem is linearly separable or not.

Question 3. By using the kernel function described in item 1, nd the vector wY by training a Support Vector Machine that reproduces the correct classification.

Hint: You may use packages like SciKit-Learn to perform this last task.

Part 2: Multilayer Networks and EBP

(a) Given the dataset in the le 'cloud.dat', formed by 1000 two-dimensional vectors r^T = (x, y), construct and train a neural network that models the probability density (y x). Report your results in form of graphs of the parameters of your models vs the variable x.

Hint: Consider a mixture model of the form:

P(y|x) = α₁(x)N (y|µ₁(x), σ₁² (x)) + α₂(x)N (y|µ₂(x), σ₂² (x)),

where 0 < α_i < 1 and α₁ + α₂ = 1 for all x.

(b) Use the maximum likelihood principle to nd the values of the parameters r⁰ and σ² in the following model:

P(r) = 1/2Π.1/√2Πσ² exp{-1/2 (r - r0)²/σ² ,

where r = x² + (y-1)².

Optimization:

Consider the functional entropy defined as

S[p] ≡ - ∫dxp(x) log p(x)

where p(x) is a well defined probability density for x∈R⁺U{0}. Suppose that all the knowledge we have about p(x) is summarized in the following properties:
1 = ∫ dxp(x)
µ = ∫ dxp(x)x

where µ∈R is known. By using the de nition of the functional derivative of a functional F (introduced in lecture 7):

δF[p]/δp(x₀) ≡ d/dλ.F[p(x) + λδ(x - x₀)]_λ=0

where p is a suitable probability density, λ ∈ R is a real number and δ(x - x0) is the Dirac's delta function centered at x₀, demonstrate that the probability density that minimizes the functional entropy (1) subject to the constraints (2) and (3) is an exponential distribution:

P(x|µ) = 1/µ.e^-x/µ.

3. Radial Basis Functions and Regularization

x	y
0	0.4556
0.1	0.8110
0.2	0.9515
0.3	0.8871
0.4	0.8281
0.5	0.4509
0.6	0.2219
0.7	0.1530
0.8	0.1501
0.9	0.2019
1.0	0.5981

Table 1: Data set for problem 3 b).

(a) Consider general Gaussian basis function of the form:

φ_j(x) =1/2Π √det(Σ) exp {-1/2 (x - µ_j)^TΣ^-1(x - µ_j)}

Σ =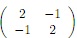

Show that the mapping represented by such a network is equivalent to a that of a function:

 

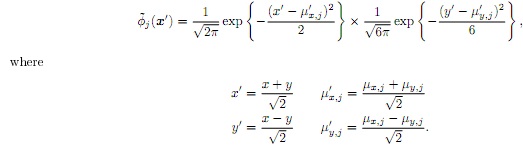
(b) Implement the radial basis network function with Gaussian kernels (with variance σ² = 0.1)) that interpolates the data set presented in Table 1.