Reference no: EM133289897

Artificial Intelligence

Purpose: To gain a thorough understanding of the working of an agent that uses Markov Decision Processes (MDP) to implement a ride sharing application. The taxi agent should pick up passengers and drop them off at 3 designated fixed points (L1, L2 and L3) in a 5 ×5 grid. Each episode of the ride sharing application involves 2 passengers P1 and P2. Each passenger is picked up from one of the 3 locations and dropped off at one of the 2 remaining locations (it is meaningless to pick and drop off a passenger at the same location). The MDP is used to generate an optimal pick up and drop off schedule for any given pair of passengers. Figure 1 provides an example of the grid and the designated locations.

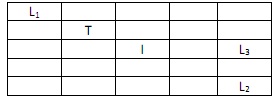
Figure 1: Designated pick up and drop off locations of passengers with an example taxi location T

In Figure 1 passenger P1 is at location L1 and has requested a drop off point of L3, while passenger P2 at location L2 has requested a drop off at L1. The Taxi is shown at location T but note that the taxi is free to move to any of the 25 locations in the grid unlike the passenger locations which are fixed. There is another fixed location I where extensive road works are being undertaken and hence is illegal to traverse.
The objective is to construct a policy P such that the agent picks up and drops off the pair of passengers in their chosen locations while ensuring that the path traversed is kept to a minimum. This involves picking the right order in which to pick up and drop off passengers as suboptimal choices will either lead to illegal pick-ups/drop offs and/or elongated (unnecessarily long) paths. See the MDP strategy document for details.

We shall refer to a journey made by the agent to service a pair of customers as an episode. For each episode we shall train the MDP to obtain the optimal path. Thus, Figure 1 represents an episode. The training will involve running the Value Iteration algorithm a certain number of times. In order to keep the running time within reasonable bounds, we shall execute 10 iterations per episode and force convergence at the 10th iteration instead of relying on the usual ? threshold for convergence.
You may make use of the code given in Tutorial 3 for the Value Iteration algorithm. Please do not use the environment given in Tutorial 3 as it is for a very different environment (although it may seem to be similar). Define your environment according to the requirements of the ride sharing application.

Likewise, do not use Q learning instead of MDP - there are a few Q learning implementations on the Web that solve a version of this problem that only consider a single passenger and hence are totally inappropriate; also, the ability to represent stochastic actions are absent in these implementations).

Environment Description: The environment is key to solving this problem. The environment consists of 5 key factors: the states, the transitions between states, the rewards to be used and finally the discounting factor Y.

1. A state in this application consists of a 5 tuple (T, P1P, P2P, P1D, P2D) where T is the location of the taxi in the grid, P1P is the pickup point for passenger 1, P2P is the pickup point for passenger 2, P1D is the drop-off point for passenger 1 and P2D is the drop-off point for passenger 2. Thus, for example for the episode given in Figure 1 we have: ((2,4), (1,5), (5,1), (5,3), (1,5)) using the convention of indexing first by column and then by row (to maintain consistency with the class notes; also, indexes start from 1 instead of 0 as in Python).

From our definition of a state, we see that we have a total of 25×3×3×2×2=900 states (we have 2×2 at the end instead of 3×3 as drop-off points need to differ from pick-up points).

2. In terms of actions, we have a total of 6 actions from each state. The set of actions A = {N, S, W, E, P, D} where N refers to North, S to South, W to West, E to East, P to Pick-up and D to Drop-off.

3. We will define the transitions between states in terms of probabilities Pr(s'|s,a) which is the probability of moving from the current state s to a new state s' using action a.

The probability matrix Pr is defined using 2 rules:
I. For a designated pick-up/drop-off location (a,b) we have: Pr((a,b)|(a,b), P)=0.4
Pr((a,b)|(a,b), D)=0.4
Pr(s'|(a,b), M)=0.05 where M ={N,S,W,E} and s' is the neighbor of s defined by action M.

II. For all other points,
Pr(s'|(a,b), M)=0.8 where M is the intended move which can be one of N,S, W or E. Pr(s'|(a,b), M)=0.04 where M is not in the intended direction
Pr((a,b)|(a,b), P)=0.04
Pr((a,b)|(a,b), D)=0.04

4. For pick-ups and drop-off points (i.e., L1, L2 and L3) we will set a value of +20,000. For the illegal pick- up/drop-off point I, we will set a reward of -10,000. The live-in reward is set at a value of -1.

5. We set Y=1.0

Implementation: Once you have written the code to implement the 3 rules above and integrated with the Value Iteration method given in Tutorial 3 (which you may use when it is available on Thursday) the next step is to train your MDP on episodes that you generate. Generate a total of 5 episodes, starting with the episode given in Figure 1. In addition to this episode, generate 4 other episodes. For each of these 4 episodes, generate random pick-up and drop-off points for the 2 passengers from the 3 available locations L1, L2 and L3. Likewise, generate a random location T for the taxi T from any of the grid points, taking care to avoid illegal point I.

Once each episode is generated, train the MDP by executing your Value Iteration algorithm with 10 iterations. Once the policy is generated the next step is to evaluate the policy. For policy evaluation, use location T as the starting point and follow the path defined by the policy until both passengers are dropped off. For the evaluation we shall compute the simple metric of path length (other metrics such as sum of expected discounted rewards are also possible, but we will not use them in this Project). The smaller the path length, the bigger is the reward obtained and hence we rank paths by length.

Your task in this project is to implement the following requirements. The project has a single milestone which is your code that you used and the answers to the questions below.

1. For episode 1 given in Figure 1, work out the optimal policy by hand. The optimal policy is the one that results in the shortest path that picks up and drops off both passengers without traversing illegal point I. Work out this optimal policy by hand and display the path P as a sequence of grid locations (2D coordinates) starting with the Taxi location T.

2. Run your MDP code for episode 1 and display the path given by its policy, also as a sequence of grid locations starting with T.

If your path differs from the path you constructed in 1 above, why do you think it is so?
3. Generate 4 other episodes. For each episode:
a. print out the locations of the pick-up and drop-off points and the location of the Taxi T.
b. print out the path and its length that was produced by your MDP to service the journey (i.e., the episode).