Reference no: EM13496018

1. Simulate N = 200 outcomes from the model

Y = -2 + X - X² + ε

where X ~ U[0, 1] and ε ~ N(0, 0:1²) independently. From your simulated outcomes of (X, Y ), fit a sequence of polynomial regression models to your data via least-squares, of degree n = 0, 1, 2, 3. Provide plots of your regression curves with the data superimposed, plots of the residuals, and supply your code.

2. Extend your solution to Q1, by calculating the error sum-of-squares for each regression model, determining the appropriate number of degrees of freedom for the error sum of squares, and calculating the mean error sum-of-squares. For each model, supply your calculated output, the degrees of freedom, and your code.

3. Extending Q1 and Q2, calculate the regression sum of squares associated with increasing the model degree by 1. Based on your residual plots, comment on the validity of the error model in each case. If the error model is valid, compute the appropriate F statistic for testing whether the additional term in the model is needed, together with the associated p-value. For valid tests, conclude whether or not the additional term is needed. Supply your calculated output, comments, and code.

4. Extending Q1, Q2, and Q3, for the model with the appropriate degree determined by your testing, plot a 95% confidence interval and a 95% prediction interval on the sample plot as your regression curve and the data points, assuming the variance 2
= 0:12 is known. Supply your plot and code.

5. In order to investigate the effectiveness of training programmes preparing new employees for routine tasks, 24 new employees (with the same background knowledge and experience) were randomly divided into 4 groups. Each group followed a different training programme. The table below shows the time (in hours) for each new employee to successfully complete the same test suite of routine tasks.

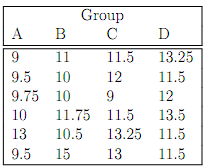
Implement a one-factor ANOVA model and compute 95% confidence intervals for the expected time taken to complete the test suite in each group. Test whether the training programmes have any effect. Supply your calculated output, comments, and code.

6. Transistor Inc. wants to investigate the effectiveness of an additional chemical bath treatment on the yield of server-grade devices. They try three new treatments, as well as their usual process. The table below lists the percentage yield of server-grade devices, for five different production plants.

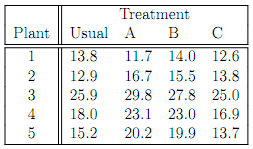
Does the data suggest that adding a chemical bath treatment makes a difference? Use two-factor ANOVA to investigate this. Supply your calculated output, com- ments, and code.