Reference no: EM131055739

1. A variable line passes through fixed point (a, b) intersecting co-ordinate axes at A and B. If 'O' is is the origin then the locus of centroid(G) of  triangle OAB is :
a) bx + ay - 3xy = 0                             
b) bx + ay - 2xy = 0                             
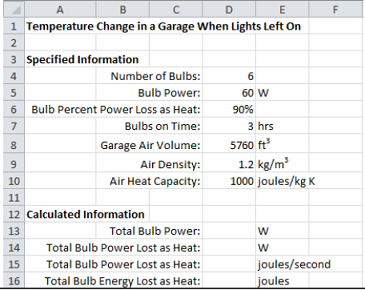
c) ax + by - 3xy = 0                             
d) None

2. The perpendicular bisector of the line segment joining P(1,4) and Q (K, 3) has Y- intercept  -4, then possible value of  k is ---
a) -4
b) 1
c) 2
d) -2

3. Number of lines that can be drawn through the point (4, -5) so that its distance from the point  (-2,3) will be equal to 12 is equal to
a) 0
b) 1
c) 2
d) 3

4. The co-ordinates of the point of reflection of the origin (0,0) in the line 4x-2y-5=0 is 
a) (1, -2)
b) (2, -1)
c) (4/5 , -2/5)
d) (2, 5)

5. The lines (a+b)x + (a-b)y -2ab =0, (a-b)x + (a+b)y -2ab =0 and x+y=0 form an isosceles triangle whose vertical angle is 
a) 90⁰
b) tan^-1(2ab/a²-b²)
c) tan^-1(a/b)
d) 2 tan^-1(a/b)

6. Two mutually perpendicular straight lines through the origin form an isosceles triangle with the line 2x+y=5. Then the area of triangle is
a) 5
b) 3
c) 5/2
d) 1

7. Consider a family of straight lines (x+y) + K(2x-y+1)=0. Find the equation of straight line belonging to this family that is farthest from (1,-3).
a) 6x-15y-7 = 0                             
b) 6x+15y-7 = 0                             
c) 5x+2y+1 = 0                             
d) 5x-2y+1=0

8. A straight line is such that its distance of 5 units from the origin and its inclination is 135⁰. The intercepts of the line on co-ordinate axes are -  

5,5
√2,√(2 )
5√(2 ), 5√(2 )
5/√(2 ), 5/√(2 )

9. In a ?ABC , if A(2,-1) and 7x-10y+1=0 and 3x-2y+5=0 are equations of an altitudes and an angle bisector respectively drawn from B, then equation of BC is
x+y+1 = 0                             
5x+y+17 = 0                             
4x+9y+30 = 0                             
x-5y-7=0

10. Let P(-1,0), Q(0,0) and R(3,3√3) be three points. Then the equation of the bisector of the angle PQR is √3/2x+y=0
x+√3 y= 0                             
√3x+y= 0                             
x+√3/2y =0

11. The x coordinate of incentre of the triangle that has the coordinates of the mid points of its sides are (1,0), (1,1) and (1,0) is

2-√2
1+√2
1-√2
2+√2

12. A straight line L through the point (3,-2) is inclined at an angle 60⁰ to the line √3x+y=1. If L also intersects the x axis, then the equation of  L is y+ √3 x+2-3√3  = 0

y-√3 x+2+3√3 = 0                             
√3 y-x+3+2√3 = 0                             
√3 y+x -3+2√3= 0

13. The point on the line 3x-2y=1 which is closest to the origin is
(3/13, 2/13)
(5/11, 2/11)
(3/5, 2/5)
(3/13, -2/13)

14. The equation of the line which passes through the point of intersection of the lines x+2y+2=0 and 2x+5y+3=0 and which is at minimum distance from point (-2,-3) is

2x+y+7 = 0

x-2y+6 = 0                             
x+3y+1 = 0                             
2x-y+3=0

15. One side of rectangle lies along the line 4x+7y+5=0. Two vertices are (-3, 1) . (1,1). Then the remaining vertices are

(1/65, -47/65), (-131/65, 177/65)
(1/65, 47/65), (-131/65, 177/65)
(1/65, -47/65), (131/65, 177/65)
(1, -4), (131, 47)

16. Consider a parallelogram whose sides are represented by the lines 2x+3y=0, 2x+3y-5=0, 3x-4y=0 and 3x-4y=3. The equation of diagonal not passing through origin is

21x-11y+15 = 0

9x-11y+15 = 0                             
21x-29y-15 = 0                             
21x-11y-15=0

17. If in triangle ABC, A(1,10) , Circumcentre (-1/3, 2/3), Orthocentre(11/3, 4/3) then the coordinates of mid-point of side opposite to A is

(1, -11/3)                             
(1,5)
(1,-3) 
(1,6)

18. Area of quadrilateral formed by the lines |x| + |y|= 2 is

8
6
4
None     

19. A straight line through the origin O meets the parallel lines 4x+2y=9 and 2x+y+6=0 at points P and Q respectively. Then the point O divides the segment PQ in the ratio

1 : 2
3 : 4
2 : 1
4 : 3

20. If 3a+2b+4c= r for some real numbers a,b,c and fixed real number r, then find the value of  'r' for which the lines ax+by+c=2 always passes through fixed point.

-6
-8
8
6

21. If the point of intersection of kx+4y+2=0, x-3y+5=0 lies on 2x+7y-3=0 then find k

a) 2
b) 3
c) -2                            
d) -3

22. If algebraic sum of the perpendicular distances from the points (2,0), (0, 2) and (4,4) to a variable line is 0, then the line passes through fixed point

a) (1,1)
b) (3,3)
c) (2,2)
d) (0,0)

23. The equation of straight line passing through the point (4,5) and equally inclined to the lines 3x=4y+7, 5y=12x+6 is

a) 9x-7y=1
b) 9x+7y=1
c) 7x-9y=1
d) 7x-9y=17

24. Consider the following statements

Statement I: The area of the triangle formed by the points A(20,22), B(21,24) and C(22,23) is same as area of triangle formed by the points P(0,0), Q(1,2) and R(2,1)

Statement II: The area of triangle remains invariant w.r.t. the translation of the coordinate axes.

a) Statement I is true, Statement II is true and Statement II is correct explanation for Statement I

b) Statement I is true, Statement II is true and Statement II is NOT the correct explanation for Statement I

c) Statement I is true, Statement II is false

d) Statement I is false, Statement II is true

25. Consider the following statements

Statement I: The quadrilateral formed by the lines x+√3y=5, √3x+y=3, x+√3y=3 and √3x+y=5 is a rhombus

Statement II: If the angle between the diagonals of a quadrilateral is 900 then it is a rhombus.

a) Statement I is true, Statement II is true and Statement II is correct explanation for Statement I

b) Statement I is true, Statement II is true and Statement II is NOT the correct explanation for Statement I

c) Statement I is true, Statement II is false

d) Statement I is false, Statement II is true

(PARAGRAPH TYPE)

Paragraph for Question Nos. 26 to 28

In the diagram, a line is drawn through the points A(0.16) and B(8,0). Point P is chosen in the first quadrant on the line through A and B. Points C and D are chosen on the x and y axis respectively, so that ? PDOC is a rectangle.

26. Perpendicular distance of the line AB from the point (2,2) is
√4
√10
√20
√50

27. Sum of coordinates of the point P if  ? PDOC is a square is
32/3
16/3
16
11

28. Number of  possible ordered pair(s) of all positions of the point P on AB so that the area of rectangle ? PDOC is 30 sq. units, is
three
two
one
zero

(MORE THAN ONE CORRECT OPTION TYPE)

29. The coordinates of the fourth vertex of the parallelogram where three of its vertices are  (-3,4), (0,-4) and (5,2) can be:
a) (8,-6)
b) (2,10)
c) (-8,-2)
d) None of these

30. If a²+9b²-4c²=6ab then the family of lines ax+by+c=0 are concurrent at:
a) (1/2, 3/2)
b) (-1/2, -3/2)
c) (-1/2, 3/2)
d) (1/2, -3/2)