Reference no: EM13809961

1. Describes four ways of defining the AI field. For each of the following sentences, state which definition of AI it seems to follow and explain your answer.

"I replaced Bob our accountant with a program. I think the program is artificially intelligent because ..."

a. "... when the program makes mistakes, it makes the same mistakes that Bob would."

b. "...all of the program's work passed inspection by our auditors."

c. "... It was programmed using the information from How to Make Managerial Accounting Decisions."

d. "... the program models Bob's actual thought processes."

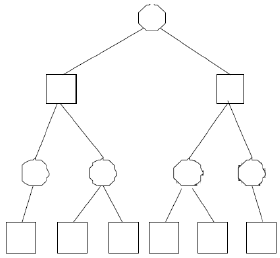
2. In the search tree shown, circles represent terminal nodes and the double circle represents the goal node. For the traversal schemes, show the node expansion order for non-terminal and non-goal nodes by placing a number near the top right of the node. Assume the search terminates when a goal is generated.

a. Breadth-first search

b. Depth-first search

3. The A* algorithm uses an evaluation function f(n) = g(n) + h(n). In one or two sentences, explain the meaning of g(n) and h(n).

4. What constraints are necessary on g and/or h* to make the A* algorithm behave equivalently to: Breadth-first, Uniform-cost, and Best-first?

5. One of your friends notices that for the A* algorithm and for the particular problem you are solving, you apply a g(n) = 1 between all nodes. He points out the fact that for all nodes at level I in the search tree, g(I) will simply equal I. Therefore, he claims, why even bother to take into account g(I)? He says, "Just forget about g(I) and let f*(n) = h*(n). Your A* algorithm will work just as good as before." Explain the fault in this reasoning.

6. Use Alpha-Beta Search to compute the final value of the root node for the tree below. Use depth-first, left-to-right progression. Be sure to:

a. identify nodes that are cut-off

b. compute the final value of the root node

Note: The root node in this tree is a min node.

Values for terminal nodes (left to right): 15 5 10 9 14 20

7. You and your chess opponent, John, are in a strange predicament. Whoever wins the present game has to play "Dirty Harry" next. It is a well-known fact that "Dirty Harry" does not fully comprehend the game of chess, moves randomly, and almost always loses. This, in itself, is not so bad; however, it is also a well-known fact that "Dirty Harry" is a very sore loser, and unless he wins, winds up shooting his opponent. Obviously, neither you nor John wants to play "Dirty Harry" next. Therefore, your strategy is to force John to win, and John's strategy is to force you to win.

a. Assuming that both you and John are consistent in choosing the worst possible move for yourselves, could you somehow adapt the alpha-beta algorithm to help you in this situation? Explain why and how, or explain why not.

b. Now, assume that the very thing you dread most has presented itself; that is, despite your best attempts to lose to John, he has managed to force you to win. Now, you are stuck in a game with "Dirty Harry." Your last hope is to play the game in such a manner that "Dirty Harry" is assured a win. Same question: could you somehow adapt the alpha-beta algorithm to help you in this situation? Explain why and how, or explain why not.

8. Given the following symbols and their meanings, translate the following propositional logic statement into English and determine whether the assertion is valid.

p: 64k is better than no memory at all.

q: We will buy more memory.

r: We will buy a new computer.

p -> (q -> r), q-> (p -> r)

(p \/ q) ->r

9. Represent the following sentences in first-order logic, using a consistent vocabulary that you define:

a. Fred works in the bank.

b. At least one person is Fred's supervisor.

c. Everyone who works in the bank handles money.

10. Suppose we have the following rules:

∀x Knows(Bill, x) =>ThreatenedBy(Bill, x)

∀xThreatenedBy(Bill, x) => Buys(Bill, x)

Suppose our knowledge base is:

∀a Knows(a, Sun)

Can we assume Bill will buy Sun? Show how we can prove this.