Reference no: EM13212236

Problem 1

(a) In the game from the previous problem set ("old lady crossing the street") identify all pure strategy Nash equilibria.

(b) In another game from the previous homework (battle of the Bismarck Sea) identify all pure strategy Nash equilibria.

Problem 2

Using only 0 and 1 as payoffs construct a 4x4 game with two pure strategy Nash equilibria.

Problem 3

To formulate the problem below I need to introduce the following definition: Consider a vector of payoffs (x, y) where x and y are payoffs to Row and Column respectively; we will say that (x*, y*) is "better" than (x, y), or equivalently that (x, y) is "worse" than (x*, y*), if x* > x and y* > y. For example, the Prisoner's Dilemma game in lecture notes is an example of a game with one Nash equilibrium in pure strategies where the vector of payoffs in this equilibrium is "worse" than some other vector of payoffs in the game. Now, using only 0, 1, 2, 3 and 4 as payoffs:

(a) Construct a 3x3 game in which there is only one Nash equilibrium in pure strategies and the vector of payoffs in this equilibrium is "worse" than some other vector of payoffs in the game. (b) Construct a 3x3 game in which there are two Nash equilibria in pure strategies and the vector of payoffs in one Nash equilibrium is "worse" than the vector of payoffs in the other Nash equilibrium.

(c) Construct a 3x3 game in which there are two Nash equilibria in pure strategies and the vector of payoffs in both is "worse" than some other vector of payoffs in the game.

Problem 4

Suppose that political ideologies can be represented on a 5 point discrete scale. The scale identifies five clearly distinguishable ideologies on a spectrum from the far left (1) to the far right (5). Assume that your electorate is evenly spread over the whole political spectrum with 20% identifying with each of the five ideologies. The only two political parties that are about to form (the country is a new democracy) can choose their ideologies anywhere on the 5 point scale. We assume that voters will vote for party that is closest to their ideology and if both parties are in equal distance the voters will split evenly between them.

Model this situation as a game. Represent payoffs as percent of votes a party gets (the other party gets the remaining percentage of votes).

(a) Solve the game through iterated dominance.

(b) To get the solution in (a) do you need to assume cardinal payoffs or ordinal payoffs would be sufficient? In other words, to arrive at the equilibrium in (a) do you merely need to assume that parties prefer more votes over less or that they also have to prefer 40% over 20% twice as strongly as 30% over 20%?

Problem 5

(1) Write out all (pure) strategies of each player in the three games below. Also, for each game (2) mark in bold all branches that will be taken at each node, (3) circle the payoffs the players will get in equilibrium, and (4) write a pair of strategies that constitute the rollback
equilibrium.

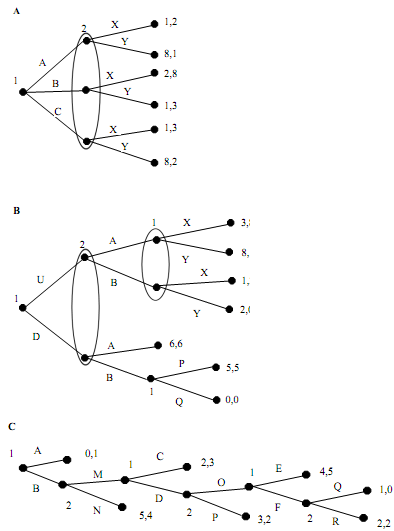
Problem 6

Assume the same situation as in Problem 4 above with a different distribution of voters: 16%, 16%, 26%, 26%, 16% in each ideology from 1 to 5 respectively. Model this situation as a game. Again, represent payoffs as percent of votes a party gets.

Can you solve this game through iterated dominance? Does the model and the analysis make sense for ordinal payoffs only, cardinal payoffs only, or both?

Assume now that the distribution of voters is 10%, 10%, 10%, 60%, 10% in each ideology from 1 to 5. Can you solve this game through iterated dominance?

Any general observations from what you have observed in all three cases.