Reference no: EM13161135
Question 1
Two astronauts Yuri and Valentina are flying their rockets towards each other, both at a speed of 0:9c as measured by observers on Earth.
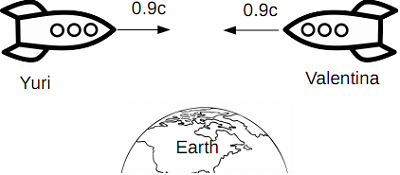
Yuri �res a laser beam towards Valentina.
(a) What is the speed of the laser beam relative to Yuri?
(b) What is the speed of the laser beam relative to Valentina?
(c) What is the speed of Valentina's rocket, relative to Yuri?
Quantum Mechanics
An electron is con�ned to a one-dimensional box of size L.
(d) Sketch the wavefunction (x) for the two lowest energy levels n = 1 and n = 2.
(e) Sketch the probability density p(x) corresponding to these two wavefunctions. Indicate the most likely positions for the electron to be found.
(f) An electron is initially in the n = 1 state. Give an example of a process by which the electron might be excited into the n = 2 state. Include in your answer a discussion of the role of the di�erence in energy between these two states.
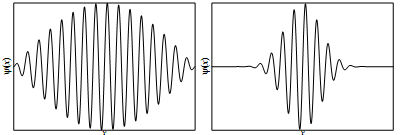
(g) The �gure below shows two wavefunctions, for particle A and particle B. Which particle has the largest momentum, and why?
Question 2
Two (�fictional) heavy particles are �red towards each other in a linear accelerator. Particle 1, moving towards the right, has a rest mass m1 = 16mp (mp is the proton mass) and velocity v1 = 3c/5 in the laboratory frame. Particle 2, moving towards the left, has a rest mass m2 = 9mp. The particles collide elastically and form a metastable particle, stationary in the laboratory frame.
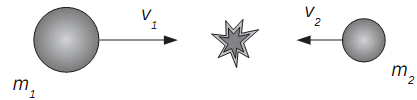
(a) Show, using conservation of total momentum before and after the collision, that the velocity of particle 2 in the laboratory frame is given by v2 = 4c/5.
(b) What is the mass of the metastable particle after the collision, in units of proton mass? Is mass conserved in the collision?
Now consider a reference frame co-moving with particle 1.
(c) In this reference frame, what is the velocity of particle 2?
(d) The rest mass is Lorentz invariant, and therefore independent of the choice of reference frame. Use conservation of energy and momentum in this new reference frame to prove that the collision will result in a particle of the same mass given by your answer to part (b) above, and moving to the left with velocity v1.
After some period of time, the metastable particle decays into a shower of lighter particles, including protons, electrons, neutrinos and photons.
(e) According to quantum mechanics, the shower of particles will scatter in all directions with equal probability. Is it possible to determine in advance the trajectory of any individual particle? Why?
f) Some particles pass through a double-slit positioned near the point of the collision. Describe (e) According to quantum mechanics, the shower of particles will scatter in all directions with equal probability. Is it possible to determine in advance the trajectory of any individual particle? Why?
(f) Some particles pass through a double-slit positioned near the point of the collision. Describe what happens as individual particles pass through it.
(g) Briefly describe how the resulting interference pattern will di�er for the various types of particles passing through: protons, electrons, neutrinos (mass close to zero) and photons. Assume that the distribution of particle energies is the same for each kind of particle.