Reference no: EM131032724

1. In general which of the following algorithms requires the most extra memory when running?

a) Insertion sort

b) Merge sort

c) Quick sort

d) Shell sort

e) All wold use the same amount of extra memory.

2. Which of the following algorithms runs in 0(AP) average time?

a. insertion sort

b) merge sort

c) quick sort

d) heap sort

e) none of the above

3. Which of the following algorithms runs in 0(N log N) average time but quadratic worst-case time?

a) insertion sort

b) merge sort

c) heap sort

d) Shell sort

e) quick sort

4. The -median-of-three" partitioning strategy is often used in a QuickSort implementation because:

a) The Quicksort always needs three pivot values

b) It helps prevent "degenerate input" sequences from degrading the algorithm's performance. C) The array is usually of an unknown length

d) It prevents empty arrays from crashing the system

e) The median value will never have to be swapped to a new location.

5. Which algorithm provides the best "real-world" performance on data that is already sorted or "mostly" sorted

a) InsertionSort

b) MergeSort

c) HeapSort

d) ShellSort

e) QuickSort

6. Which algorithm provides the most consistent performance when sorting data. (The actual number of operations is the most independent of the input order of the data.)

a) InsertionSort

b) HeapSort

C) QuickSort

d) None are affected significantly by the original ordering.

e) All can vary greatly, depending on order of the supplied data.

7. If an arbitrary item is added to the end of an already sorted list, how much time will it take to sort the array again using insertion sort?

a) o( 1 )

b) 0( log N )

c) 0( N )

d) O (N log N )

e) 0( N² )

8. Which of the following is true about the height of a node?

a) The height of a node is always one less than the height of its parent

b) The height of an empty tree is 1

C) The height of a leaf is always 0

d) The maxim height of a tree can be larger than its maximum depth

e) all of the above are false

9. Insertions and lookups on a Hash-map may operate in 0(1) time whereas Search Tree's require 0(log n) time. BRIEFLY explain: How/why Hash-maps may operate in a lower computation complexity than Tress and why Trees might still be preferable over Hash-maps in many cases.

10. List the following algorithms in order from Slowest to Fastest (in terms of their general "real world" AND theoretical average performance) and provide the key reason why each successive algorithm is faster than its predecessor; no more than 5 or so words! If there is a "tie", indicate such briefly mention why.

QuickSort, BubbleSort, MergeSort, HeapSort, SelectionSort, ShellShort, InsertionSort, CountingSort.

11. The first stage of a Heap-Sort is to represent an input sequence as a "Binary Heap", Given a list (4, 3, 1, 2, 9, .6,. 7, 8, 5)

a) Show the "Binary MAX Heap" Representation (assuming the items are added to the heap in the order given) as both a tree and as a new array.

"Heap" Array:

9

8

7

6

5

4

3

2

1

b) Show the Heap after the removal of the largest element (eg. the first item positioning of the "Heap Sort".)

"Heap" Array:

9

8

7

6

5

4

3

2

1

12. The two nodes marked *'s in the tree below have a height difference greater than one (two, to be precise). Does the tree have the structural properties of a valid AVL tree? Why or why not?

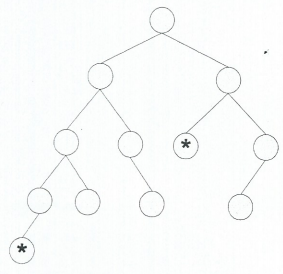
The next four questions relate to the tree below:

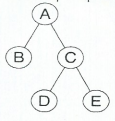
1. Which of the following traversals yields ABCDE?

a) inorder

b) level (bredth) order

C) postorder

d) preorder

e) two of the above

2. Which of the following is an inorder traversal of the tree?

a) ABCDE

b) ABDCE

c) BDECA

d) EDCBA

e) none of the above

13. Using the following tree:

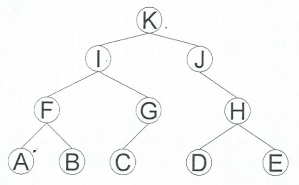
a) Show a post-order traversal (the nodes as they are displayed) of the above tree

b) Show a pre-order traversal (the nodes as they are displayed) of the above tree

C) Show an in-order traversal (the nodes as they are displayed) of the above tree

14. Show the resulting .AVL Tree after the insertion of the following elements - in order - into a new AVL tree: 30, 20, 10, 5, 6, 15, 2

15. Assuming a Quick Sort, where a first element of any "sub array" is always the pivot show the resulting array after the first "pivot value" has been swapped into it's correct location (ie, after the first partitioning of the array into the first two "sub arrays"):

[4, 1, 7, 8, 6, 9, 3, 5, 0]

16. Assuming an radix sort is used to sort the elements below. Show each of the resulting "intermediate" arrays as the array is placed into sorted order.

[123, 122, 222, 111, 132, 133]

17. Assume characters have the following values: a=1, b=2, c=3, d=4, e=5 and a string hashing function that simply adds the character values and mods with 5: (₀∑^k Char_k)mod 5

For example "abae" = (1+2+1+5)965 => 4

Show the addition of the following strings to a "Closed" Hash table (in order):

"abc" , "bbb" , "cb", "ee", "abcde"

0
1
2	abc
3	cb
4	bbb
5	ee
6	abcde

18. Show the addition of the following strings to an "Open" Hash table (in order): "abc", "bbb", "cb" , "ee", "abcde"