Reference no: EM131106498

Honors Exam 2011 Statistics

1. At age 35, 1 in 270 pregnant women carry a fetus with Down syndrome.

(a) An article in the November 10, 2005 issue of the New England Journal of Medicine reports the results of a large study on first-trimester screening for Down syndrome (using measurements of nuchal translucency, PAPP-A, and fβhCG). Among 8,199 women subjects with singleton pregnancies who were at least 35 years of age, exactly 64 carried fetuses with Down syndrome. Among those 64, 95 percent tested positive on the screening test; among the other 8,135, 22 percent tested positive. Estimate the probability that a 35 year old woman (with a singleton pregnancy) who tests positive on the screening test has a fetus with Down syndrome, and state any assumptions needed to justify your calculation.

(b) An article in the April 21, 1994 issue of New England Journal of Medicine reports on the study of a large cohort of pregnant women age 35 or older who were undergoing routine amniocentesis (an invasive procedure that definitively reveals whether or not a fetus has Down syndrome). Of the 54 high risk women who were found to have a fetus with Down syndrome, 48 also tested positive on serum markers. Find an approximate 95% confidence interval for the proportion of high risk women age 35 or older carrying a fetus with Down syndrome who tests positive on serum markers. Do you think your approximation is good?

2. Let X and Y be independent and exponentially distributed, µ_X = E(X) and µ_Y = E(Y). (An exponential distribution with mean µ has pdf f (x) = 1/µ e^-x/µ for x ≥ 0.) Suppose

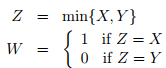
(a) Find P (Z ≤ z and W = 0) and P (Z ≤ z and W = 1).

(b) Prove that Z and W are independent. (Hint: Show that P (Z ≤ z |W = 0) = P (Z ≤ z) and P (Z ≤ z |W = 1) = P (Z ≤ z).)

(c) Let (Z₁, W₁), . . . , (Z_n, W_n) be a random sample from the joint distribution in (a). Find MLEs for µ_X and µ_Y.

3. Thirteen computer-proficient medical professionals were timed both while retrieving an image from a library of slides and while retrieving the same image from a database of digitized images with a Web interface. The table below gives the retrieval times (in seconds):

Subject	1	2	3	4	5	6	7	8	9	10	11	12	13
Slide	30	35	40	25	20	30	35	62	40	51	25	42	33
Digital	25	16	15	15	10	20	7	16	15	13	11	19	19

At least how much more quickly can digital images be retrieved? Use the data above to answer at the 95% confidence level; justify, if possible, any assumptions you make.

4. Let X₁, . . . , X_n be independent Poisson(λ) random variables. (For λ > 0, the Poisson(λ) distribution has pmf p(x) = e^-λ (λ^x/x!) for x ∈ {0, 1, 2, . . .} .)

(a) What are the mean and variance of a Poisson distribution with parameter λ?

(b) Suppose you have prior information that λ ∼ Gamma(α, β). Find the posterior distribution.

(c) What is the mean of the posterior distribution (the "posterior mean of λ")? What is the maximum posterior estimate of λ (the value of λ at which the "mode" of the posterior density occurs)?

5. Suppose the number of dandelion plants in a square meter is Poisson distributed, with parameter λ₁ in Region 1 and parameter λ₂ in Region 2. For 125 quadrates (square meter plots) in Region 1 and 140 quadrates in Region 2, the table below gives the number of dandelion plants per quadrate.

	0 plants	1 plant	2 plants	3 plants	4 plants	5 plants	6 plants	7 plants
Region 1	29	38	31	19	4	3	0	1
Region 2	18	31	33	29	13	10	5	1

(For example, 19 of the quadrates sampled from Region 1 have exactly 3 dandelion plants each.) Find an approximate 95% confidence interval for λ₁ - λ₂, and state any assumptions needed to justify your calculation.

6. The data below are based on information provided by W. Stanley Jevons in 1868. In a study of coinage, he weighed 274 gold sovereigns that he had collected from circulation in Manchester, England. For each coin, he recorded the weight-after-cleaning to the nearest .001 gram, and the date of issue. The table below lists the average, miniumum and maximum weight for each age class. The age classes are coded 1 to 5, roughly corresponding to the age of the coin in decades.

Age (decades)	Sample Size n	Average weight	SD	Minimum weight	Maximum weight
1	123	7.9725	.01409	7.900	7.999
2	78	7.9503	.02272	7.892	7.993
3	32	7.9276	.03426	7.848	7.984
4	17	7.8962	.04057	7.827	7.965
5	24	7.8730	.05353	7.757	7.961

The standard weight of a gold sovereign was supposed to be 7.9878 grams; the minimum legal weight was 7.9379 grams.

(a) Do these data suggest that it is appropriate to use ordinary least squares to model the relationship between age and weight of gold sovereigns? If there are model assumptions that you can't check using just the information above, please state them.

(b) Model the relationship as best as you can, and use the data above to estimate model parameters.

(c) Is the fitted model consistent with the known standard weight of a new gold sovereign? Provide the details of an appropriate hypothesis test.

(d) For a previously unsampled coin in each age group, estimate the probability that the weight of the coin is less than the legal minimum. (Use the standard normal distribution, not t distributions, to calculate the probabilities.)