Reference no: EM131366226
Assignment
1. Graph the linear inequality. x+2y ≥ -4
Use the graphing tool to graph the inequality.
2. Graph the feasible region for the following system of inequalities. Tell whether the region is bounded or unbounded.
x + 4y ≤ 16
4x + 5y ≥ 20
Use the graphing tool on the right to graph the system of inequalities.
Is the region bounded or unbounded?
unbounded
bounded
3. Graph the feasible region for the system of inequalities. Tell whether the region is bounded or unbounded.
-1 < x < 2
-1 ≤ y ≤ 3
2x + y < 5
Use the graphing tool to graph the system.
The region is (1) _____
bounded.
unbounded.
4. A dietician is planning a snack package of fruit and nuts. Each ounce of fruit will supply 1 unit of protein, 2 units of carbohydrates, and 1 unit of fat. Each ounce of nuts will supply 1 unit of protein, 1 unit of carbohydrates, and 1 unit of fat. Every package must provide at least 7 units of protein, at least 12 units of carbohydrates, and no more than 10 units of fat. Let x equal the ounces of fruit and y equal the ounces of nuts to be used in each package.
a. Write a system of inequalities to express the conditions of the problem.
b. Graph the feasible region of the system.
a. Fill in the chart.
|
|
Fruit
|
Nuts
|
Requirements per
package
|
| Protein |
____ unit(s) per ounce
|
____ unit(s) per ounce
|
At least ______ unit(s)
|
| Carbohydrates |
____ unit(s) per ounce
|
____ unit(s) per ounce
|
At least ______ unit(s)
|
| Fat |
____ unit(s) per ounce
|
____ unit(s) per ounce
|
No more then _____ unit(s)
|
Let x be the number of ounces of fruit and y the number of ounces of nuts. Referring to the chart, give the three inequalities that x and y must satisfy because of the package's requirements for protein, fat, and carbohydrate.
____ ≥ 7
____ ≥ 12
____≤10
Give the inequalities that x and y must satisfy because they cannot be negative.
Y ≥ ____
x ≥ ____
b. Graph the feasible set for the packaging problem. The feasible set is shaded.
5. The graph shows a region of feasible solutions. Use this region to find maximum and minimum values of the given objective functions, and the locations of these values on the graph.
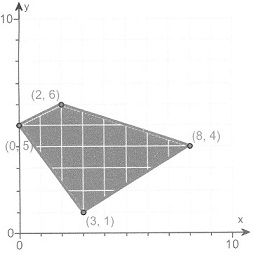
(a) z = 6x + 3y
(b) z = x + 9y
(a) What is the maximum of z = 6x + 3y? Select the correct answer below and, if necessary, fill in the answer boxes to complete your choice.
A. The maximum value of the objective function z = 6 _______ and is located at the point ________. (Type an exact answer.)
B. The maximum does not exist.
What is the minimum of z = 6x + 3y? Select the correct answer below and, if necessary, fill in the answer boxes to complete your choice.
A. The minimum value of the objective function z = 6 ______ and is located at the point ______. (Type an exact answer.)
B. The minimum does not exist.
(b) What is the maximum of z = x + 9y? Select the correct answer below and, if necessary, fill in the answer boxes to complete your choice.
A. The maximum value of the objective function z = x and is located at _____. (Type an exact answer.)
B. The maximum does not exist.
What is the minimum of z = x + 9y? Select the correct answer below and, if necessary, fill in the answer boxes to complete your choice.
A. The minimum value of the objective function z = x and is located at _____. (Type an exact answer.)
B. The minimum does not exist.
6. Solve the following linear programming problem.
Maximize: z = 7x + 3y
subject to: 4x - y ≤ 14
2x + y ≥ 13
x ≥ 3
y ≤ 9
The maximum value is ____. (Type an integer or a simplified fraction.)
The maximum occurs at the point ________. (Type an ordered pair. Type an integer or a simplified fraction.)
7. Write the constraint below as a linear inequality.
A canoe requires 3 hours of fabrication and a rowboat 7 hours. The fabrication department has at most 86 hours of labor available each week. Let x be the number of canoes and let y be the number of rowboats.
Choose the inequality that represents the given constraint.
A. 7x + 3y ≤ 86
B. 3x + 7y ≤ 86
C. 3x + 7y ≤ 86
D. 7x + 3y ≥ 86
8. A dairy company gets milk from two dairies and then blends the milk to get the desired amount of butterfat. Milk from dairy I costs $2.40 per gallon, and milk from dairy 11 costs $0.80 per gallon. At most $144 is available for purchasing milk. Dairy I can supply at most 50 gallons averaging 3.7% butterfat, and dairy II can supply at most 80 gallons averaging 2.9% butterfat. Answer parts a and b.
a. How much milk from each supplier should the company buy to get at most 100 gallons of milk with the maximum amount of butterfat?
The company should buy _____ gallons from dairy I and __________ gallons from dairy 11.
What is the maximum amount of butterfat?
______ gallons. (Type an integer or a decimal.)
b. The solution from part a leaves both dairy I and dairy Il with excess capacity. Calculate the amount of additional milk each dairy could produce.
The excess capacity of dairy 1 is ______ gallons, and for dairy II it is _______ gallons.
Is there any way all this capacity could be used while still meeting the other constraints? Explain.
A. No. Any more milk purchased from either dairy will go over budget.
B. Yes, 10 more gallons can be bought from dairy I and 20 more from dairy II without going over budget.
C. Yes, 10 more gallons can be bought from dairy ! without going over budget.
D. Yes, 10 more gallons can be bought from dairy I without going over budget.
9. A patient takes vitamin pills. Each day he must have at least 600 IU of vitamin A, 8 mg of vitamin B1, and 25 mg of vitamin C. He can choose between pill 1, which contains 420 IU of vitamin A, 2 mg of vitamin B1, and 5 mg of vitamin C, and pill 2, which contains 60 IU of vitamin A, 2 mg of vitamin B1, and 10 mg of vitamin C. Pill 1 costs 30¢, and pill 2 costs 15¢. Complete parts a and b below.
a. How many of each pill should he buy in order to minimize his cost? What is the minimum cost?
He should _______ buy of pill 1 and ______ of pill 2. The minimum cost is $ ________. (Simplify your answers. Type integers or decimals.)
b. For the solution in part a, the patient is receiving more than he needs of at least one vitamin. Identify that vitamin, and tell how much surplus he is receiving.
He is receiving _______ 1U of vitamin A, _______ mg of vitamin B1, and ________ mg of vitamin C more than he needs. (Simplify your answers.)
Is there any way he can avoid receiving that surplus while still meeting the other constraints and minimizing cost? Explain. Choose the correct answer below.
A. Yes. Take one fewer of each pill to reduce the cost.
B. No. Reducing the surplus would either cause the cost to increase or cause the patient to receive less than needed of another vitamin.
C. Yes. Reverse the numbers of each pill taken.