Reference no: EM13884501

1) A 1.4 kg falling object (subject to the effects of aerodynamic drag) is 1800 m high, traveling at 34 m/s and has not yet reached terminal speed. It first reaches terminal speed at a height of 1340 m and the terminal speed is 37.3 m/s.

a) Determine if the mechanical energy ( E = K + U_g ) of the system consisting of the falling object and Earth's gravity field has been conserved during the fall from 1800 m to 500 m.

b) How much work (if any) including the correct sign (+ or -­) has been done on the system over this interval (presumably by the external drag force)?

c) Will the energy of the system consisting of the object, the gravity field and the surrounding air be conserved over this interval? Explain your answer. Is there an additional energy that must be accounted for in this analysis? What is it and how much of it has been generated? Note: terminal speed is a constant speed.

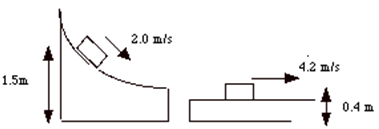
2) The 0.2 kg box below slides down a curved ramp, jumps a small gap and lands on a flat platform. At the point on the ramp shown it is 1.5 m above the floor and its speed is 2.0 m/s. At the point shown on the platform the box is 0.4 m above the floor and sliding at 4.2 m/s.

a) If we consider a system consisting of the box and Earth's gravity field so that E = K + U_g , has the energy of this system been conserved during the described process? Explain how you know.

b) If we consider the exact same process but broaden our system definition so that E = K + U_g + E_other and E_other  includes any "other" form of energy that might have been produced through the process (most of it is thermal), what objects are included in this system? Discuss, don't just state a list.

c) Determine ΔE_other for the process as described.

d) How much kinetic energy would the box have on the platform if ΔE_other  = 0 ?

3) The system below consists of two masses attached through a string of negligible mass over a pulley that turns with negligible friction.  m₁  > m₂ and the sphere  m₂  is immersed in a viscous fluid that exerts a considerable drag force. Starting from rest the system is set into motion by releasing m₁ which causes this mass to descend while the other rises (assume the string instantly becomes taut). In what follows analyze the motion by defining the "system" as both masses and Earth's gravity field.

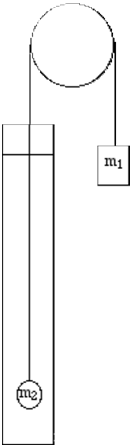
a) Once released each mass travels a distance h1 and somewhere during this interval both masses reach terminal speed VT . Write out (derive/formulate) a mathematical expression for the change of the potential energy of the system over this interval (Using the givens! Don't make up numbers or define your own variable names.) Has the system gained or lost potential energy? Explain how you know.

b) Write out (derive/formulate) a mathematical expression for the change in the kinetic energy of the system over the h1 interval (using the givens). Write out an expression for the work done by the drag force over this interval using the givens.

c) Following the h1 interval the system moves a distance h2 while the sphere is still immersed in the fluid. Write out an expression for the work done by the drag force over this interval. Can you tell from this expression if the work done by drag is positive or negative? (You should.) Which is it and how do you know?

d) If h1 = h2 over which interval does the drag force do more work in an absolute value sense? How do you know?

4) A 48 kg diver jumps off a cliff (with a running start) into the ocean. The cliff is 50 m above the ocean below. Her coach, using a video of the dive, determines that at a point in flight when she has risen 0.7 m above the cliff, her speed1 (center of mass) is 0.5 m/s. Frictional effects such as drag are negligible.

Formulate your solution using the diver and Earth's gravity field as a system. Gravity does not do work on this system. It's effects are captured in changes in potential energy.

a) How much kinetic energy did she have at takeoff?  What was her speed?

b) How much kinetic energy will she have as she splashes into the ocean?

c) What minimum amount of chemical energy needed to be consumed within the diver's body in order for her to walk to the cliff, from ocean level, and then take off (jump)? Explain how you know.