Reference no: EM132845243

Question 1. Apply the method of inclusion-exclusion to do the following:

(a) How many ways are there to arrange the letters of CHEDDARCHEESE so that no pair of consecutive letters are the same?
(b) Find the number of 6 digit positive integers whose digits sum to 21. [Beware of leading zeroes!]
(c) Find an expression for the number of solutions to x₁ + . . . x_k = m, where each x_i is a positive integer between 1 and t and use the expression to show that

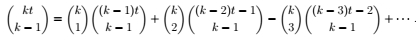
Question 2. (a) For 1 ≤ i ≤ n, let Ti be the subset of the n × n square board containing the squares indexed (s, t), where 1 ≤ s ≤ i and 1 ≤ t ≤ s. (i.e. Ti is a triangle-shaped board).
i. Find r_k(T_i) for i ∈ {1, 2, 3} and each k ≥ 0.
ii. For i ≥ 1, find and prove an expression for the rook polynomial R(x, T_i).

(b) Imre was so delighted by Shoham's hospitality that he decides to have a (small) dinner party. He invites Antonio, Marthe, Shoham and Richard. Imre is a cheese connoisseur. He orders 5 very special cheeses for the occasion: St Felicien, Brillat Savarin, Marianne, Roquefort and Gorgonzola. Somewhat bizarrely, instead of cutting the cheeses up and sharing them, Imre wants to serve each guest an entire cheese.

Unfortunately, some of his guests have dietary restrictions. Marthe will only eat cheese which is French (St Felicien, Brillat Savarin). Shoham is very polite, she knows some of the guests love St Felicien and Brillat Savarin, so she declines these options. Richard's yoga teacher has a bad feeling about blue cheese, so he won't eat the Gorgonzola or Stilton. Imre's favourites are the Brillat Savarin, St Felicien, Stilton and Marianne, so he would like to serve himself one of these. Antonio would like to hide his lack of knowledge about cheese, so he requests that he not receive the Brillat Savarin (even though he does not know what this is).

i. Draw a board which depicts the cheese preferences of the guests at the dinner party.
ii. Calculate how many possible options Imre has to serve the cheeses according to the restrictions. [Using the result from 2a might save you some time here.]
(c) Find two different boards with the same rook polynomial, and the property that neither can be obtained from the other by row and column permu- tations.

Question 3. Some of the guests at Imre's party are doubtful as to whether they can eat an entire cheese. Imre, a good host, swiftly decides that perhaps it is better to cut the 5 cheeses into slices after all. He has a large circular cheeseboard with places for 15 pieces of cheese equally spaced around the edge. He quickly chops all the cheeses up and places slices around the board. Two arrangements are considered to be equivalent if they differ up to rotation.

(a) Let G be the group of possible permutations of the cheeseboard. Find the cycle index polynomial.

(b) How many non-equivalent arrangements of cheeses are possible. (As- sume that Imre has cut each cheese up into at least 15 slices, so there are no restrictions on how many slices of each cheese there are.)

(c) How many non-equivalent arrangements are there that contain an equal number of slices of each cheese.

Question 4. After dinner, the 5 people decide to have a croquet competition. Each pair of people plays a match and there are no ties (so each match has a winner and a loser). Two outcomes of the competition are equivalent if one can be obtained from the other by permuting the names of the participants. E.g. The outcome where Antonio beats ev- eryone, Shoham beats all but Antonio, Richard beats all but Antonio and Shoham and Imre beats Marthe, is equivalent to the outcome where Imre beats everyone, Shoham beats all but Imre, Marthe beats all but Imre and Shoham, and Richard beats Antonio.

(a) If only 3 people participate, how many non-equivalent outcomes are there?
(b) Apply Burnside's Lemma to determine how many non-equivalent out- comes there are for the competition involving all 5 people.

Question 5. (a) Say that two numbers are equivalent if reading one upside down is the other. E.g. 189 and 681 are equivalent. How many non-equivalent n letter words can be made from the symbols {0, 1, 6, 8, 9}.
(b) i. Find the number of equivalence classes of functions f : Z₂³ → Z₂
where f is equivalent to g if f (x, y, z) = g(y, z, x).
ii. How non-equivalent functions send seven elements of the domain to 0 and one to 1?

Bonus question Pick any topic from the course as inspiration for a creative endeavour. This could take the form of a haiku, limerick, song, poem, sculpture, interpretive dance...