Reference no: EM13722201

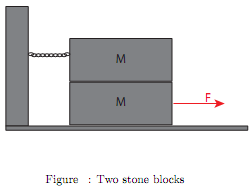
Problem I: Two stone blocks with mass m = 100 kg are stacked as shown in figure on a stone surface. The top block is held in place by a chain and cannot move to the right. The coefficient of static friction between the blocks, and between the lower block and the surface, is µ_s = 0.6. What is the minimum force F necessary to begin sliding the lower block out from under the stack?

Problem 2: A child of mass m = 20 kg goes down a slide at a playground. She starts at a height h = 2.2 m with zero velocity. Assuming zero friction, how fast will she be going at the bottom?

Problem 3: When you do the experiment in the previous problem, you measure the child's final speed to be 1.8 m/s, which is lower than the answer you might expect. Explain where the "missing" energy went, describe the other force that did work on the child, and calculate how much work that force did.

Problem 4: A "normal" spring has a force equation given by Hooke's law: F_s = -kx. This is known as a "linear" spring, for reasons that are obvious if you look at the equation long enough. It's quite possible to build a "non-linear" spring: they're useful in things such as the suspensions on racing motorcycles, for example.

F_s = -k₁x - k₂x³

The normal linear spring force is conservative, so it has a potential function U_s(x) = ½ kx². Is the nonlinear spring conservative, and if so, what is its potential function?

Problem 5: A cyclist (mass m) is racing around a flat circular track of radius r at constant speed v.

(a) Frictional force between the track and the bike tires provides the centripetal force necessary to go in a circle. How much work is done by friction in exactly half a lap?

(b) If the cyclist stops in exactly half a lap, how much work is done by friction during the stop?

Problem 6: The Bugatti Veyron is -let's just admit it- ridiculous. Never mind "Zero to Sixty" time: this car can go from zero to one hundred and fifty miles per hour in just 9.8 seconds. And that's despite a mass of 1900 kg!

(a) What is its average acceleration during a 0-150 drag run?

(b) What is its average power during a 0-150 drag run?

Problem 7: One problem Tarzan had to deal with while swinging on vines is that vines grow on trees. He started swinging one one such vine (L = 14 m) with an initial angle of θ_i = -20^o, measured from vertical. When he reached an angle θ_f = +4^o, he met a tree face-first. How fast was he going? Assume that Tarzan's mass was 80 kg.

Problem 8: One area of human endeavor that would seem to require a thorough understanding of conservation of energy is bungie jumping. You have a bungie cord with a spring constant k = 700 N/m and an unscratched length L_o = 40 m. Your mass is (for this problem) m = 70 kg. How high a bridge do you need?

Problem 9: The mass in a spring / mass system is displaced by a distance x_o.

(a) Calculate the work done by the spring in bringing the mass back to x = 0.

(b) Find the maximum speed for this system, using techniques from the previous homework set. (Simple Harmonic Motion! x = x_o cos ωt, etc.) Using this maximum speed, calculate the maximum kinetic energy, and compare with part (a).

Problem 10: Use Python to plot a graph of position v. time for ping-pong ball in free-fall. It's time for real physics now; we will not assume air resistance is zero! For "reasonable" speeds, drag force in air is

F_d = ½Cρ Av²

C is the drag coefficient which depends on the shape of the object, ρ is the density of the air, and A is the cross-sectional area of the object. Let's simplify and combine all those constants into one number:

F_d = -ßv² where ß = 2.2 x 10^-4 Ns²/m². Since the drag force F_d depends on speed v, the acceleration of a dropped ping-pong ball is not constant. We can still use Euler's method, though. In fact, we could use the same code as was presented last week in Python Problem #4; we'd just have to replace the acceleration a = g in the line v=v - g * dt with the new acceleration

a = ( g- (ß/m) v² )

where m = 0.0025 kg is the mass of a ping-pong ball.

So do it! For this problem turn in a graph showing position v. time for a ping-pong ball dropped from an initial height of 10 m, for the first two seconds of the ball's motion. Show the constant-acceleration approximation on the same graph, and put your name in the title.

Problem 11: Bubba is driving hid truck at speed v. The combined mass of Bubba and truck is m.

a) If Bubba stops truck without skidding I distance D_a, how much work is done by friction?

b) If Bubba laks the brakes and skids to a stop in distance D_b, how much work is done by friction?

c) If Bubba goes around a flat corner of radius D_c, while maintaining his speed v, how much work is done by friction?