Reference no: EM131146447

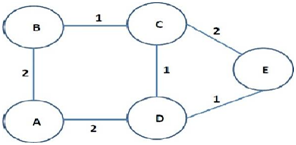
1. We have discussed Dijkstra's algorithm in class for computing the shortest paths from any source node to all other nodes in a network. The first step is to codify the network information, i.e., how do we represent the link costs? One way is to use a matrix representation. If the link costs have been expressed as a matrix C, then the (i, j)th element of the matrix gives the cost of the link between i and j (obviously, if i = j, Cif = 0, for all i). For example, the cost matrix for the network shown in Fig. 1 is (first row/column is for node A, second row/column is for node B, etc.):

You can assume that the user would not make any error in entering the link cost matrix (i.e., the matrix would be symmetric, non-negative, and al elements along the leading diagonal will be 0). That is, your code does not need to check for potential errors in the link cost matrix.

Write a function computeDijkstra(sourceID,C)' which takes as inputs the source node ID and the link cost matrix and returns the final best cost vector and the final predecessor vector.

For example, referring to slide-38 of Chapter-5 notes, your out¬put arguments should be [0,2,3,1,2,4] and [A, A, E, A, D, El or [1,1,5,1,4,5] if you label each node by a numeric, i.e., [A, B, C, D, E] -4 [1,2,3,4,5].

The pseudocode is available on slide-36 of Chapter-5 notes.

1. Consider the 6-node network shown in Fig. 1. The numbers shown next to the edges (links) represent the link costs. Using Dijkstra's algorithm, find out the minimum cost paths from node. A to all other nodes in the network. In your homework, you should include a table similar to the one shown on slide 38 of Chapter-5 notes (make sure to show both the minimum cost vector p as well as the predecessor vector). [25 points)

If you cannot implement the predecessor vector, just try to return the final cost vector. You can earn up to 50 points if you do so correctly.

You cannot use built in functions which directly compute the shortest path tree or implement Dijkstra's algorithm.

Here's a MATLAB tip. Suppose x = [2, 3, 1, 4, 5]. Executing (a,b) = min(x) returns a=1 and b=3. The parameter b therefore returns the position in x where the minimum is found.

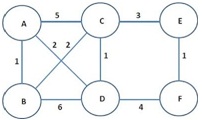
Figure 1: Network for Problem 1.

NOTE: You should email me your codes with instructions on how to rim than.

1.Consider the 6-node network shown in Fig. 1. The numbers shown next to the edges (links) represent the link costs. Using Dijkstra's algorithm, find out the minimum cost paths from node. A to all other nodes in the network. In your homework, you should include a table similar to the one shown on slide 38 of Chapter-5 notes (make sure to show both the minimum cost vector p as well as the predecessor vector). 

2. In some cases, link costs reflect reliabilities. In this case, the definition of a best cost path changes. For example, the reliability of the path A -+ B -> C is defined as: r(ARC) = r(A13) x r(BC), i.e., the reliability of it path is the product of the reliabilities of the hops constituting the path. In addition, the reliability measure of a link is a number between 0 (actually, a very very small number, say, 10 10 0) and 1. If the reliability of a link is 0.8, you can interpret that as `the probability that the link will fail is 0.2'. In contrast, if the link costs were to be viewed as dollar costs (or even delays in seconds), you would add up the costs of the hops constituting a path to obtain the cost of that path.
When link costs are modeled as reliabilities, a certain mathematical transformation allows you to convert products of individual reliabilities to sums of transformed reli-abilities. What is that transformation' After the tnumformation, what is the nature of an link costs (maximum and minimum limits)? In Dijkstra's algorithm, we seek to find paths which minimize the sum of link costs. Noting that finding the minimum of -x (where x is an arbitrary variable) is equivalent to finding the maximum of x, explain how you could adapt Dijkstra's algorithm when link costs reflect reliabilities. After you have thought it out, find the most reliable paths from node A to all other nodes for the network shown in Figure 2. in points]
Even though you are not being asked to do anything about this, it is worth¬while to note that there's an alternate definition of the reliability of a path. Just as a chain is only as strong as its weakest link, the reliability of a path is sometimes also defined as the minimum of the reliabilities of the hops constituting a path. Under this definition, if the reliability of the link (A, B) is 0.8 and the reliability of the link (B,C) is 0.2, then the reliability of the path (A 14 B 44 C) is the minimum of 0.8 mid 0.2, or, 0.2. By the definition of the first paragraph, however, the reliability of the path (A i4 B H C) is 0.8 x 0.2 = 0.16.

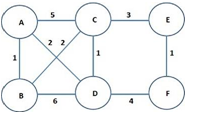
3. The network shown in Figure 3 is in operation. Distance vector protocol is used for routing. 
(a) Construct the routing tables at each of the five nodes.
(b) Subsequently, the cost of the link (A, D) changes to 5. Node D is the first to detect this and updates its routing table. It then sends out an advertisement to nodes A, C and E. In response, nodes A, C and E update their own routing tables and inform their neighbors (i.e., node A sends to B and D; node C sends to B, D and B; and node E sends to C and D). This process continues until routes/costs have stabilized. If you think this through, you will see that node A's first two routing table updates are in response to: (i) an update from D, and then, (ii) an update from B. Construct the routing tables at A after each of these two steps. In order to answer this, you might have to construct the routing tables at other nodes.