Reference no: EM131109117

2009 Honors Examination: Real Analysis

I. Basic Analysis

1. (a) Define the terms "compact" and "complete," as they apply to a metric space.

(b) Show that in a compact metric space, any sequence has a convergent subsequence.

(c) Show that if a Cauchy sequence has a convergent subsequence then the sequence itself is convergent.

(d) Show that any compact metric space is complete.

2. (a) Prove that the sum _n=0Σ^∞(xⁿcos(nx)/n!) converges for all x ∈ R. Prove that it does not converge uniformly on the real line, but nevertheless defines a continuous function on R. State precisely any theorems you use.

(b) How about the sum of the derivatives? Does it converge pointwise? Does it converge uniformly on R? Does it converge to the derivative of the function studied in (a)? Once again, state precisely any theorems you use.

3. Let f(t) be the "inch-long ruler function" defined on the interval [0, 1] by

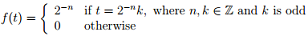
(a) Where is f(t) continuous?

(b) Is f(t) Riemann integrable? If so, what is its integral?

II. Analysis on Manifolds

4. (a) Let A be a subset of Rⁿ. Define what is meant by "A is of measure zero," "the boundary of A," and "the closure of A."

(b) If A has measure zero, must its closure have measure zero? Must its boundary have measure zero? Provide proofs or counterexamples.

5. For what values of a, b is the surface defined by w² + x² + y² + z² = a and wxyz = b a submanifold of R⁴? State precisely any theorems you use in proving your claim. Give an equation of the tangent plane at (1, 2, 3, 4) to the surface in this family which contains that point.

6. (a) Give an example of a smooth 2-form ω₀ on R³ - {0} (where 0 is the origin) which is closed (i.e. dω₀ = 0) but not exact. (Hint: in terms of vector fields, you might want to consider a vector field of the form r^→/r^p for some p.)

(b) Let a, b ∈ R and let p, q be distinct points in R³. Use the form ω₀ to define a smooth 2-form ω on R³ - {p, q} which is closed but has the property that if S_p is a sphere centered at p with radius ||p - q||/2, S_q is defined analogously, and both are oriented so that the "positive" side is out, then

∫_{S_p} ω = a,            ∫_{S_q} ω = b .

If I give you a smooth closed surface S in R³ such that p ∉ S and q ∉ S, what do you have to know in order to compute ∫_S ω?

7. Let H be the upper hemisphere in R³,

H = {(x, y, z) : x² + y² + z² = 1, z ≥ 0} ,

with normal vector pointed outward. Compute ∫_H z dx ∧ dy.