Reference no: EM131094939

Question 1. Two-particle wave function

In a one-dimensional problem, consider a system of two particles (1) and (2) with which is associated the wave function ψ (x₁, x₂).

a. What is the probability of finding, in a measurement of the positions X1 and X2 of the two particles, a result such that:

x ≤ x₁ ≤ x + dx

α ≤ x₂ ≤ β

b. What is the probability of finding particle (1) between x and x + dx [when no observations are made on particle (2)] ?

c. Give the probability of finding at least one of the particles between α and β.

d. Give the probability of finding one and only one particle between α and β.

e. What is the probability of finding the momentum of particle (1) included between p₁ and p₂ and the position of particle (2) between α and β.

f. The momenta P₁ and P₂ of the two particles are measured; what is the probability of finding p' ≤ p₁ ≤ p"; p"' ≤ p₂ ≤ p""?

g. The only quantity measured is the momentum P₁ of the first particle. Calculate, first from the results of e and then from those of .1, the probability of finding this momentum included between p' and p". Compare the two results obtained.

h. The algebraic distance X₁ - X₂ between the two particles is measured; what is the probability of finding a result included between - d and + d? What is the mean value of this distance?

Question 2. Infinite one-dimensional well

Consider a particle of mass m submitted to the potential:

V(x) = 0 if 0 ≤ x ≤ a.

V(x)= +∞ if x < 0 or x > a.

| φ_n > are the eigenstates of the Hamiltonian H of the system, and their eigenvalues are E_n = n²Π²h²/2ma² (cf. complement H₁). The state of the particle at the instant t = 0 is :

|Ψ(0) > = a₁ (Ψ₁ > + a₂ |(Ψ₂ > + a₃ l (Ψ₃ > + a₄|(Ψ₄ >

a. What is the probability, when the energy of the particle in the state |Ψ (0)> is measured, of finding a value smaller than 3Π²h²/ma²?

b. What is the mean value and what is the root-mean-square deviation of the energy of the particle in the state |Ψ(t)>?

c. Calculate the state vector |Ψ(t)> at the instant t. Do the results found in a and b at the instant t = 0 remain valid at an arbitrary time t?

d. When the energy is measured, the result 8Π²h²/ma² is found. After the measurement, what is the state of the system? What is the result if the energy is measured again?

Question 3. Infinite two-dimensional well (cf. complement G_II,)

In a two-dimensional problem, consider a particle of mass m; its Hamiltonian H is written :

H  = H_x + H_y

with:

H_x = px²/2m + V(X)    H_y = px²/2m + V(Y)

The potential energy V(x) [or V(y)] is zero when x (or y) is included in the interval [0, a] and is infinite everywhere else.

a. Of the following sets of operators, which form a C.S.C.O. ?

{ H },{H_x}, {H_x, H_y} {H, H_x}

b. Consider a particle whose wave function is:

Ψ(x, y) =  N cos Πx/a.cos Πy/a.sin2Πx/a.sin2Πy/a

when 0 < x < a and 0 < y < a, and is zero everywhere else (where N is a constant).

α. What is the mean value < H > of the energy of the particle? If the energy H is measured, what results can be found, and with what probabilities ?

β. The observable H_x is measured; what results can be found, and with what probabilities? If this measurement yields the result Π²h²/2ma², what will be the results of a subsequent measurement of H_y, and with what probabilities?

γ. Instead of performing the preceding measurements, one now performs a simultaneous measurement of H_x and P_y. What are the probabilities of finding:

E_x = 9Π²h²/2ma²

and :

P_o ≤ P_y ≤ p_o + dp ?

Question 4. Consider a physical system whose state space, which is three-dimensional, is spanned by the orthonormal basis formed by the three kets |u₁ >, |u₂ >, | u₃ >. In this basis, the Hamiltonian operator H of the system and the two observables A and B are written:

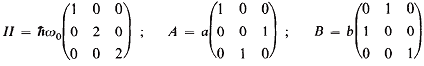
where ω_o, a and b are positive real constants.

The physical system at time t = 0 is in the state:

|Ψ(0) > = 1/√2 |μ₁| > + 1/2 |μ₂> + 1/2|μ₃>

a. At time t = 0, the energy of the system is measured. What values can be found, and with what probabilities? Calculate, for the system in the state 0(0) >, the mean value < H> and the root-mean-square deviation ΔH.

b. Instead of measuring H at time t = 0, one measures A; what results can be found, and with what probabilities? What is the state vector immediately after the measurement?

c. Calculate the state vector |ψ(t)> of the system at time t.

d. Calculate the mean values < A > (t) and < B > (t) of A and B at time t. What comments can be made?

e. What results are obtained if the observable A is measured at time t? Same question for the observable B. Interpret.

Question 5. Interaction picture

(It is recommended that complement F_III and perhaps complement G_III be read before this exercise is undertaken.)

Consider an arbitrary physical system. Denote its Hamiltonian by H_o(t) and the corresponding evolution operator by U_o(t, t'):

Now assume that the system is perturbed in such a way that its Hamiltonian becomes :

H(t) = H_o(t) + W(t)

The state vector of the system in the "interaction picture", |Ψ_I(t)> is defined from the state vector |Ψ_I(t) > in the Schrodinger picture by :

|ψ(t)> = U_o⁺(t, t_o)W(t)U₀(t,t₀)

a. Show that the evolution of I 1P/(t)> is given by :

i^hd/dt|ψI(t)>| = WI(t)|ψ_I(t)>

where W₁(t) is the transform operator of W(t) under the unitary transformation associated with U₀^t(t, t_o)

W₁(t) = U₀^t(t, t_o),W(t) U_o(t, t_o)

Explain qualitatively why, when the perturbation W(t) is much smaller than H_o(t), the motion of the vector |ψs(t)>. is much slower than that of |ψ_s(t)>.

b. Show that the preceding differential equation is equivalent to the integral equation :

|ψ_I(t)> = |ψ_I(t_o)> + 1/ih_to∫^tdt'WI(t')|ψ_I(t'))>

where : |ψ_I(t_o) > = |ψ_s(t)>.

c. Solving this integral equation by iteration, show that the ket |ψ_I(t)> can be expanded in a power series in W of the form: