Reference no: EM132958873

UBGMUA-15-M Nonlinear Structural Analysis - University of the West of England

Task 1 - Generation of elastic response spectrum

Acknowledgement: This assessment uses ground motion acceleration data, which is publicly available to download via the Pacific Earthquake Engineering Research Center (PEER).

Consider the ground motion time history signal shown in Fig.1. As earthquake loading is not a deterministic load (i.e. it cannot be described analytically) and is highly transient, a corre- sponding structural response is often calculated with the use of a response spectrum.

A response spectrum is a plot of period versus acceleration, which shows the maximum re- sponse of a linear single degree of freedom (SDOF) system for a given component of an earth- quake ground motion. Using MATLAB or other general programming language you are asked to generate an elastic response spectrum based on ground motion data. Fig.2visually illus- trates the generation process of a response spectrum. Each point in the spectrum corresponds to the peak response of a SDOF with a specific natural period Tn.

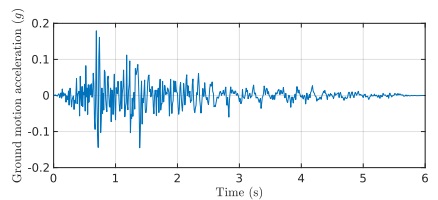
Figure 1: Acceleration time history response

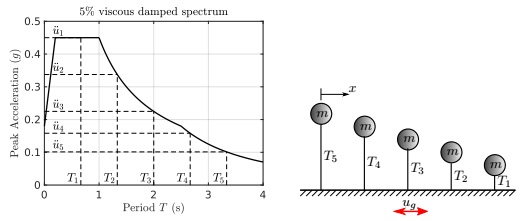
Figure 2: a) 5 % damped elastic spectrum according to EC8, and b) single degree of freedom systems with different natural periods (from left to right the oscillator is stiffer and therefore has a lower period).

In this assignment you are asked to compute the displacement, velocity and acceleration response spectra for a given ground motion, considering the period range between 0.1 s and 4 s. In this assignment you are asked to compute the displacement, velocity and acceleration re- Consider also that the oscillator is initially at rest and has a damping ratio ζ = 5 %. Keeping the mass constant, vary the stiffness of the oscillator to obtain the desired period.

As mentioned above, the response of a structure subjected to ground motion has no analytical form, and has therefore to be approximated numerically. There are numerous methods avail- able, each with different levels of convergence, stability and accuracy. For the present assign- ment you will be primarily supported to implement and use Newmark's method. You are free to use any routine available online, as long as you provide appropriate reference. However, extra marks will be awarded if you are able to implement and justify the use of an alternative method.

The ground motion shown in Fig.1is an example for illustration - you have been assigned a data set that is individual to you and whose filename is listed in column 2 of Table1. Your data file can be downloaded directly from Blackboard. Note that each data file has header lines (to be ignored), five columns of acceleration data (only the first column is to be considered), data

The following workflow is suggested

1. Carry out the validation process by implementing the analytic solution first. Implement the transient and steady state responses separately. If necessary, start considering a single harmonic of the total load and then progress to add the other two;
2. Validate the analytic solution against the provided solution and then against the numer- ically approximated solution;
3. Read and post-process the ground motion data into your programming environment.
4. Use your validated method to approximate the response of a SDOF driven by ground motion, within a loop which changes its dynamic properties (period).
5. Plot the vectors of peak acceleration, velocity and displacement response against each period that you have generated. The resulting plots are the elastic response spectra for your ground motion/SDOF.

Task 2 - Seismic design of a steel framed structure

In this task you are asked to carry out a seismic analysis and design a steel framed structure against a seismic event using Autodesk Robot software or other FE package, see Fig.4. You have to design the structure following the guidelines prescribed in the Eurocode 8 for a nonlin- ear pushover analysis. To support the design of your steel framed structure, you are expected to produce a report (1200 words) including CAD/BIM drawings of the designed frame.

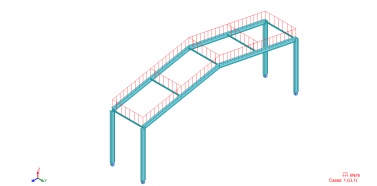
Figure 4: Autodesk Robot model of a steel frame with two portals.

1 Requirements

The structure should have the following geometrical/material requirements:

• have a specific number of portals that is individual to you and is listed in column 3 of Table1;
• have a minimum distance between portals of 2.5 m;
• have a minimum clear height of 4.2 m;
• each portal of the frame should have a clear span of 8 m;
• you have to consider the self-weight of the structure, a dead load of 4 kN/m and a live load of 1.6 kN/m on the roof beams.
• be made of steel grade S235 with a perfectly plastic material model.

The following workflow is suggested

1. Pre-design your structure based on the geometrical/material requirements and vertical loads;

2. Model your structure in a specialised FE software to obtain its capacity curve;

3. Separately, use the Annex B of the EC8 to determine the target displacement that your structure has to reach, using the required response spectrum for the above seismic action;

4. If the pushover curve stops before the target displacement, the structure has to be re- designed so that its limit displacement is increased, e.g., by reducing the stiffness of the system;

5. When the pushover curve stops after the target dispacement, use your FE software to calculate the internal forces at that displacement, and carry out ultimate limit state (ULS) verification (bending and shear failure checks at the minimum).

Attachment:- Nonlinear Structural Analysis - Brief exam.rar