Reference no: EM133039734

Assignment - Fuzzy Logic Models

This assignment mixes theory and application, in the form of several challenges and problems. Perform the tasks described in each. Note that this (and other) assignments include a few challenging research-related tasks. They are aimed at gradually building your capacity to tackle complex topics, familiarize yourself with academic discourse, and provide context and practice for the skills you will eventually need when working on your capstone thesis or project.

APA style is expected, as well as formal and rigorous scientific writing, using appropriate mathematical notation and references.

Part 1 - Theory

Task 1. Consider the following fuzzy model of a system with inputs x and y and output z:

Rule 1: If x is A3 OR y is B1 THEN z is C1
Rule 2: If x is A2 AND y is B2 THEN z is C2
Rule 3: If x is A1 THEN z is C3

The membership functions of the input and output variables are given in the graphs below:

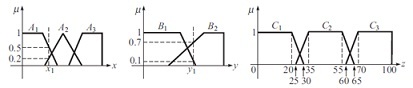
Actual inputs are x1 and y1. Find the output z by applying standard fuzzy operation:
min for AND
max for OR.

Show and explain all your steps.

Task 2. Read "Solving the Ocean Color Inverse Problems by Using Evolutionary Multi-Objective Optimization of Neuro-Fuzzy Systems" from your topic resources.

a. Explain in a short paragraph (10-15 sentences) the application/use of the Takagi-Sugeno fuzzy model in the article.
b. Explain in a short paragraph (10-15 sentences) the application/use of ANFIS.

Part 2 - Fuzzy Models

Refer to the readings assigned for this topic and provide solutions to the following problems, using Jupyter notebooks. Include formal and detailed explanations to accompany the code.

Problem 1. Consider a two-dimensional sinc equation defined by:

y = sinc (x₁, x₂) = sin(x₁) sin(x₂)/x₁x₂

Training data are sampled uniformly from the input range [-10, 10] × [-10, 10]. With two symmetric triangular membership functions assigned to each input variable, construct a Takagi-Sugeno fuzzy model (linear static mappings) for the sinc function. Provide defining equations for determination of the premise and consequent parameters of the model.

Problem 2. To identify the non-linear system

y = (1+(x₁)^0.5+(x₂)^-1 + (x₃)^-1.5)²

Assign two membership functions to each input variable. Training and testing data are sampled uniformly from the input ranges:

Training data: [1, 6] × [1, 6] × [1, 6]
Testing data: [1.5, 5.5] × [1.5, 5.5] × [1.5, 5.5]

Extract Takagi-Sugeno fuzzy rules from the numerical input-output training data that could be employed in an ANFIS model.

List and explain all the rules.

Note: You may find "Fuzzy Interference System Implementation in Python" article from your topic resources useful for this assignment. The project described is not exactly like the one you are asked to address, but it provides an adequate example of how to approach implementing a Takagi-Sugeno model in Python.