Functions of the decision variables

Reference no: EM13517678

PROBLEM :

In his previous life, Dr. Konur was a shepherd in Anatolia. He had 50 sheep that he used to shepherd. In one of those days, Dr. Konur needed to direct these 50 sheep (on the left side) across the river so that his sheep can meet with the grass (on the right side).

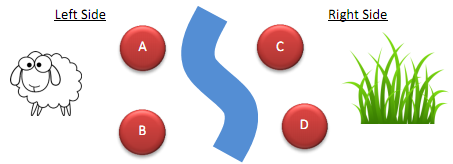
1636_Systems Engineering.png

Even if Dr. Konur was a shepherd, Dr. Konur always had some engineering skills and he spotted four points, A and B are on the left side, and C and D are on the right side of the river. Dr. Konur can build a bridge between the points on different sides of the river. That is, he can build a bridge between A and C, A and D, B and C, and B and D. However, different bridges can carry different number of sheep and it takes Dr. Konur different times to build the bridges. The table below shows the number of sheep each bridge can carry and the time required to build each bridge.

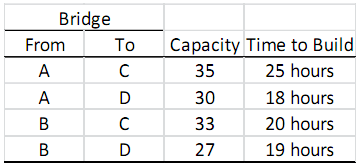
984_Systems Engineering1.png

Since Dr. Konur's sheep were very hungry, Dr. Konur wanted to build bridges as soon as possible (that is, the total time to build the bridges needed to be minimized) so that there were sufficient bridges that could carry these 50 sheep to the other side of the river. That is, Dr. Konur wanted to decide on which bridges to build so that the total time to build the bridges is minimized and the total capacity of the bridges is at least enough to carry 50 sheep to the other side. However, while solving his problem, Dr. Konur needed to be careful about the following engineering design requirements:

- From a point on the left side, there can be built at most 1 bridge to the other side.
- There can be built at most one bridge to the points on the right side of the river.

As Dr. Konur's new student in his current life, you are asked to formulate a binary-integer linear programming problem for Dr. Konur's problem as a shepherd in his previos life. Define you decision variables, and express your objectives and constraints as functions of the decision variables, and combine everything.

Reference no: EM13517678

Questions Cloud

Obtain the buoyant force acting on the balloon : A large balloon of mass 222 kg is filled with helium gas until its volume is 335 m3. Assume the density of air is 1.29 kg/m3 and the density of helium is 0.179 kg/m3. Calculate the buoyant force acting on the balloon

Formulate a mixed-integer-linear-programming model : Formulate a mixed-integer-linear-programming model for the problem above by defining the decision variables, expressing objective function and constraints as functions

Determine the plane spacing : If an X-ray beam of wavelength 1.4 × 10-10 m makes an angle of 30° with a set of planes in a crystal causing first order constructive interference, what is the plane spacing

Obtain the required maximum voltage : An inductor (L=500 mH), a capacitor (C=4.00 uF), and a resistor (R=600 O) are connected in series. Calculate the required maximum voltage

Functions of the decision variables : Define you decision variables, and express your objectives and constraints as functions of the decision variables, and combine everything.

Compute the rms value of the current in this circuit : A 120-V rms voltage at 60.0 Hz is applied across an inductor, capacitor and a 100-? resistor in series. what is the rms value of the current in this circuit

Determine the depth of the water : A person in the air above the water in a swimming pool looks straight down into the water (n = 1.33) at a diamond ring that lies on the bottom of the pool. what is the depth of the water

Explain a certain temperature mol of ca(oh)2 dissolves : 1 mol of Ca(OH)2 is placed in 2 L of water and stirred. At equilibrium, at a certain temperature, 0.0180 mol of Ca(OH)2 dissolves. What is Keq

What is the critical angle for internal reflection of a ray : Carbon disulfide (n=1.63) is poured into a container made of fused quartz (n=1.46). What is the critical angle for internal reflection of a ray in the liquid

User Account

All Pages