Reference no: EM13324847
Baklava Shipment
Dr. Konur plans to start a new business on marketing Baklavas in Rolla, MO. His father has a bakery/pastry store in Istanbul, Turkey and Dr. Konur wants to ship as much baklava as possible from Istanbul to Rolla. However, upon investigation of custom rules, he finds out that international food shipment to U.S. has the following restrictions:
- Any food shipment should arrive in New York City customs
- You cannot ship more than 120,000 baklavas through New York City
- Any food shipment originated from Istanbul should go to Paris or London before entering New York City
- If a shipment stops at Paris, it can be sent to London before being shipped to New York City; however, you cannot ship from London to Paris
Additional to these restrictions, the company that Dr. Konur wants to use for his shipments has the following limitations for baklava shipments:
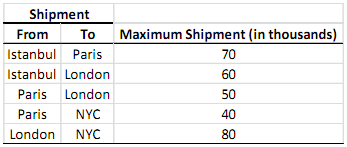
Dr. Konur knows that the maximum amount of baklavas he can send from New York City to Rolla, using the network between New York City and Rolla, is 150,000. Now he wants to find the maximum amount of baklavas that he can ship from Istanbul to Rolla given the above custom restrictions and the shipping company limitations.
Please answer the following questions based on the problem statement given above.
a) Represent Dr. Konur's problem on a network by defining the nodes, node values (if any), arcs, arc costs (if any), arc capacities (if any) and state it as a maximum-flow problem and mathematically formulate Dr. Konur's maximum-flow problem as a linear model (Hint: You will need to define a dummy node to take care of the limit that can be sent through New York customs).
b) Model the above problem using spreadsheet, i.e., on Excel and find the optimum solution using Excel solver.
About sub-paths of a shortest path
Suppose that you have a network with nodes A, B, C... Z. Furthermore, suppose that you know the shortest path from node A to node Z, denoted as A→Z. You know that this shortest path, i.e., the pat A→Z passes through node K. That is, A→Z=A→K→Z. Will the sub-path A→K be a shortest path from node A to node K? Yes or No? Explain why?
|
How knowledge is important in your system
: Write an introduction to your chosen knowledge-based system for healthcare centre
|
|
At which corner is the second charge located
: A positive point charge q is fixed in position at the center of a square. A second point charge is fixed to corner B, C, or D. At which corner is the second charge located
|
|
Explain cations while leaving the other cation in solution
: Consider a solution that is 1.1*10^-2 M in Ba2+ and 2.0*10^-2 M in Ca2+. A - If sodium sulfate is used to selectively precipitate one of the cations while leaving the other cation in solution, which cation will precipitate first? Ba2+ precipitates..
|
|
What total distance did the canister travel
: During launches, rockets often discard unneeded parts. A certain rocket starts from rest on the launch pad, What total distance did the canister travel between its release and its crash onto the launch pad
|
|
Formulate dr. konurs maximum-flow problem as a linear model
: Represent Dr. Konur's problem on a network by defining the nodes, node values (if any), arcs, arc costs (if any), arc capacities (if any) and state it as a maximum-flow problem and mathematically formulate Dr. Konur's maximum-flow problem as a lin..
|
|
Standard-form syllogism and determine whether it is valid
: Reconstruct the following as a standard-form syllogism, and determine whether it is valid.
|
|
What length of wire do you end up with
: As part of a class project you are given 0.900 g of nichrome and asked to fabricate a wire with uniform cross-section. What length of wire do you end up with
|
|
Company shifts focus to only competing in the thrift
: Suppose the Digby company shifts focus to only competing in the Thrift and Nano segments, while competing on price by reducing costs and passing the savings to the customers, what strategy would they be implementing?
|
|
Formulate a maximum-flow problem
: Formulate a maximum-flow problem that will determine the maximum number of people that can travel to the safe facilities
|