Reference no: EM13342656

PROBLEM 1: Distribution Management

Suppose that you are the distribution manager for a company. Currently, you need to plan the shipments of a product to three stores.

- Store 1 requires 50 units of the product each day
- Store 2 requires 40 units of the product each day
- Store 3 requires 70 units of the product each day

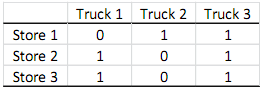
You have three trucks that you can use to make shipments to the stores. Each truck has a capacity of carrying 75 units of the product per day. Furthermore, each truck follows the same route every day. The table below shows whether a truck's route passes through a store or not (a value of 1 implies that truck passes through that store, and a value of 0 implies that the truck does not pass through that store).

That is, truck 1 can stop at Stores 2 and 3; truck 2 can stop at Store 1; and truck 3 can stop at Stores 1, 2, and 3 (the order of the stops to the stores on a truck's route is not important as the units can be loaded to the trucks accordingly). As the distribution manager, you want to determine how to load each truck by deciding on how many units of the product will be delivered to each by each truck. While doing so, you need to make sure that each store is delivered with exactly the number of units of the product they require. Furthermore, due to unloading operations, a truck cannot deliver more than 50 units per day to the same store. For instance, if truck 1 is loaded with 60 units, it cannot delivery all 60 units to store 3.

As the distribution manager, you want to make the shipment plan to minimize the total daily cost. Total daily cost is equal to the sum of the truck costs. Due to different total distances of the truck routes, truck 1 costs $10 per unit loaded, truck 2 costs $9 per unit loaded, and truck 3 costs $11 per unit loaded.

(Assume that you can ship fractional number of units to any store with any truck.)

a) Mathematically formulate a linear programming model for the above distribution management problem. Define your decision variables and the notation you use for them, express the objective and objective function, and constraints using your decision variables.

Combine everything to get the final linear model.

b) Mathematically formulate the following constraints:

a. The number of units delivered to Store 1 with truck 3 should be greater than or equal to the number of units delivered to Store 1 with truck 2.

b. Truck 3 should carry more than 40% of the total units carried by trucks 1 and 2.

c. You cannot deliver to Store 3 with truck 1.

c) Now suppose that you want to minimize the total weekly cost. Would the optimum solution of the model you formulated in part a change? Explain your reasoning briefly without solving the model in part a and the model with the weekly cost minimization.