Reference no: EM13517663

PROBLEM 1:

Dr. Konur the Shepherd

In his previous life, Dr. Konur was a shepherd in Anatolia. He had 50 sheep that he used to shepherd. In one of those days, Dr. Konur needed to direct these 50 sheep (on the left side) across the river so that his sheep can meet with the grass (on the right side).

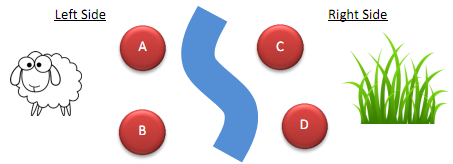
Even if Dr. Konur was a shepherd, Dr. Konur always had some engineering skills and he spotted four points, A and B are on the left side, and C and D are on the right side of the river. Dr. Konur can build a bridge between the points on different sides of the river. That is, he can build a bridge between A and C, A and D, B and C, and B and D. However, different bridges can carry different number of sheep and it takes Dr. Konur different times to build the bridges. The table below shows the number of sheep each bridge can carry and the time required to build each bridge.

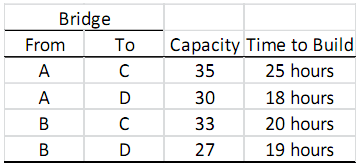
Since Dr. Konur's sheep were very hungry, Dr. Konur wanted to build bridges as soon as possible (that is, the total time to build the bridges needed to be minimized) so that there were sufficient bridges that could carry these 50 sheep to the other side of the river. That is, Dr. Konur wanted to decide on which bridges to build so that the total time to build the bridges is minimized and the total capacity of the bridges is at least enough to carry 50 sheep to the other side. However, while solving his problem, Dr. Konur needed to be careful about the following engineering design requirements:

- From a point on the left side, there can be built at most 1 bridge to the other side.
- There can be built at most one bridge to the points on the right side of the river.

As Dr. Konur's new student in his current life, you are asked to formulate a binary-integer linear programming problem for Dr. Konur's problem as a shepherd in his previos life. Define you decision variables, and express your objectives and constraints as functions of the decision variables, and combine everything.

PROBLEM 2: Manufacturing Strategy

Suppose that you are the manufacturing strategy developer of a company. Right now, you need to determine where and how to produce a product. Specifically, you need to produce exactly 8,750 units of the product for the next period. There are three plants that you can use for manufacturing the product. Each plant has a fixed payment that you have to pay to use (if you do not pay this fixed payment, you cannot use the plant). The table below shows the fixed payment for each plant.

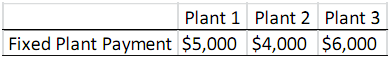
Once you select the plants that you will use for manufacturing, you need to decide how many machines to place in each selected plant. You can place at most 5 machines in each plant (if you do not pay the fixed payment for a plant, you cannot place any machine in that plant). Placing a machine in different plants has different fixed costs. The table below shows the cost of one machine placement in each plant.

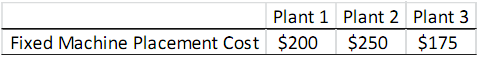
For instance, if you plan to use plant 1, you will pay $5,000 as the fixed plant payment, and you will pay $200 for each machine you place in plant 1. Each machine can produce at most 1,000 units. That is, the machine capacity does not depend on the plant in which the machine is placed (any machine can produce at most 1,000 units wherever it is placed). For instance, if you place 2 machines in plant 3, you can produce at most 2,000 units in plant 3. However, if you decide to use a plant for manufacturing, you have to produce at least 1,500 units in that plant.

Once you know the number of machines in a plant, it is not important how many you produce with each machine in that plant as the production cost per unit is the same for the machines in the same plant. For instance, if you place 3 machines in plant 2, and you decide to produce 2,500 units in plant 2, it does not matter how much of these 2,700 units will be produced with the first, second, or third machines (each can produce 900 or first and second machines produce 1000 while the third machine produces 700) since the unit production cost for each machine within the same plant is the same. However, the unit production cost in each plant is different due to different locations of the plants. The table below shows the production cost per unit produced in each plant.

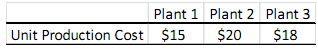
As the manufacturing strategy developer, you need to determine which plants to operate in, how many machines to place in each plant, and how much to produce in each plant so that you can minimize the total costs (plant payments + machine placement costs + production costs) while producing 8,750 units.

Formulate a mixed-integer-linear-programming model for the problem above by defining the decision variables, expressing objective function and constraints as functions of your decision variables and combining everything to get the final formulation.

Note 1: The number of machines placed in a plant should be non-negative integer. The number of units produced in a plant can be fractional.

Note 2: Your model should consist of linear functions only.

PROBLEM 3: Track Inspection Planning

Dr. Konur has recently completed a project for Missouri Department of Transportation, which was for optimizing the track inspection planning on the Missouri railroad network. In this question, you are asked to formulate a simpler version of the track inspection planning problem.

In particular, suppose that there 5 rail tracks that you can inspect. Each track has different inspection importance and each track has different inspection times. The table below gives the importance level and inspection time for each track.

As the inspection planner, you want to determine which tracks to inspect such that you maximize the total importance level of the inspections. However, you have one day, i.e., 24 hours available for inspections. That is, total inspection time cannot exceed 24 hours.

a)  Formulate a binary linear programming model for the above inspection planning problem by defining you decision variables and writing the objective and objective function and the constraints in terms of your decision variables. Combine everything to get the final model.

b) Mathematically formulate the following restrictions as constraints independent of each other and the constraints in part a. You should formulate a single constraint for each part.

a. You have to inspect at least 3 tracks.
b. If you inspect track 1, then you have to inspect track 2.
c. You can either inspect track 3 or track 4, but not both.
d. If you inspect both track 1 and track 2, then you have to inspect track 4.
e. You cannot inspect track 3 unless you inspect track 4.
f. You cannot inspect track 1 unless you inspect track 3; and, you cannot inspect track 3 unless you inspect track 1.

c) Mathematically formulate the following restrictions as constraints independent of each other and independent of the constraints in parts a and b (you might need more than one constraints in some parts or you might need to define new decision variables in some parts).

a. If you inspect track 3, you can inspect at most 2 other tracks.
b. If inspect 1 or less tracks, then track 4 cannot be inspected. That is, track 4 cannot be the only inspected track.
c. If you inspect 1 or more tracks, you have to inspect at least 2 tracks.

PROBLEM 4 : Dr. Konur the Sherriff

Dr. Konur is the Sherriff of Rolla and right now he needs to assign policemen to the different shifts.

There are 50 policemen he can assign a shift. There are 4 different shifts:
- Shift 1: Starts at 6:00am and ends at 6:00pm
- Shift 2: Starts at noon and ends at midnight
- Shift 3: Starts at 6:00pm and ends at 6:00am
- Shift 4: Starts at midnight and ends at noon
Since different shifts have different start and end times, assigning a policeman to different shifts has different costs. Specifically, a policeman costs $100, $110, $150, and $175 in shifts 1, 2, 3, and 4, respectively. Also, there should be a specific number of policemen available in different time periods to make Rolla safe. The minimum numbers of policemen needed for each time period are given in the table below.

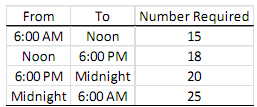
Since Rolla is on a tight budget, Dr. Konur wants to minimize the total cost of the police station he is managing by determining the integer number of policemen to assign to each shift such that at least the minimum number of policemen required in each time period is available for each time period.

a) Mathematically formulate an integer linear programming model for Dr. Konur's problem by defining your decision variables, and expressing your objective and objective function, and constraints using your decision variables. Combine everything to get the final formulation.

b) Answer the following questions independent of each other and without solving the problem and explain your reasoning briefly.

a. If Dr. Konur could assign a fractional number of policemen to any shift, would that increase costs? Yes or No or Maybe? Explain your answer briefly.

b. If Dr. Konur had to assign at least 20 policemen to shift 1, would that increase costs? Yes or No or Maybe? Explain your answer briefly.