Reference no: EM13372393

For the following demand function.

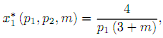
for values of m > 1.

a. Obtain Income elasticity of demand. Plot the Engel curve for p₁ = 1.

b. Is this a normal good?

c. Assuming that preferences are monotonic (then the individual always spends all its income), use the budget constraint to solve for x₂* (p₁, p₂, m).

d. The consumer faces the following prices and income level.

prices p₁ = 1, p₂ = 1.5 and income m = 5.

Calculate the quantity demanded for goods 1 and 2 at these prices and this income level.

e. Obtain income and substitution effects with Slutsky compensation when the price of good 1 drops to p_i = 0.5

Part-2

Assume preferences can be represented by the following utility function.

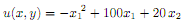
a. Is the utility function monotonic? Justify.

b. Set up the consumerís utility maximization problem for prices p₁, p₂ and income m (the general case)
c. Solve the problem. You will obtain demand functions x₁* (p₁, p₂, m) and x₂* (p₁, p₂, m) in terms of the parameters (p₁, p₂, m).

d. Graph the demand function for good 1 when the price of good 2 is p₂ = 2 and income is m = 200.

e. Obtain the change in consumer surplus when the price of good 1 goes from p₁ = 2 to p₁ = 4.

f. Again, assuming the price of good 1 increases to p_i = 4. Find the Compensating and the Equivalent Variations

g. For the same price increase, obtain the income and substitution effects on good 1, both with Slutsky and Hicks compensations.