Find values of six trigonometric functions for given angle

Assignment Help Mathematics

Reference no: EM13975915

1. Find the values of the six trigonometric functions for the angle θ. Assume a = 7, b = 24, c = 25.

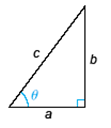
2. Find the values of the six trigonometric functions for the angle θ. Assume a = 1, c = 4.

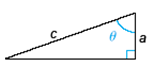
3. Find the values of the six trigonometric functions for the angle θ.

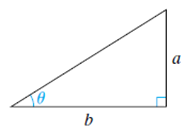
4. Find the values of the six trigonometric functions for the angle θ.

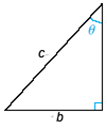
5. Find the exact values of x and y. Assume s = 4.

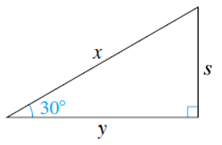
6. Find the exact values of x and y. Assume a = 9.

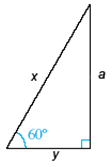
7. Find the exact values of x and y. Assume s = 8.

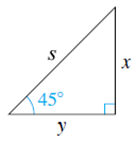
8. Find the exact values of the trigonometric functions for the acute angle θ. sin θ= 4/5

9. Find the exact values of the trigonometric functions for the acute angle θ. cos θ = 12/13.

10. Find the exact values of the trigonometric functions for the acute angle θ. tan θ =3/4.

11. Find the exact values of the trigonometric functions for the acute angle θ. cot θ = 24/7.

12. Find the exact values of the trigonometric functions for the acute angle θ. sec θ =8/7.

13. A forester, 150 feet from the base of a redwood tree, observes that the angle between the ground and the top of the tree is 55°. Estimate the height of the tree. (Round your answer to one decimal place.)

14. Use the Pythagorean identities to write the expression as an integer.

(a) tan² 9β - sec² 9β

(b) 9 tan² β - 9 sec² β

15. Use the Pythagorean identities to write the expression as an integer.

(a) csc² 6α - cot² 6α

(b) 6 csc² α - 6 cot² α

16. Use the Pythagorean identities to write the expression as an integer.

(a) 8 sin² θ + 8 cos² θ

(b) 8 sin²(θ/4) + 8 cos² (θ/4)

17. Use fundamental identities to write the first expression in terms of the second, for any acute angle θ. cos θ, cot θ

18. Find the exact values of the six trigonometric functions of θ if θ is in standard position and the terminal side of θ is in the specified quadrant and satisfies the given condition.

III; parallel to the line 2y - 9x + 7 = 0

19. Find the exact values of the six trigonometric functions of θ if θ is in standard position and the terminal side of θ is in the given quadrant and satisfies the given condition.

II; Parallel to the line through A(-1, 10) and B(-2, 13)

20. Find the exact values of the six trigonometric functions of each angle, whenever possible. (If there is no solution, enter NO SOLUTION.)

(a) 900°

(b) -810°

(c) 10π

(d) 9π/2

21. Find the quadrant containing θ if the given conditions are true.

quadrant I
quadrant II
quadrant III
quadrant IV

(a) cos θ < 0 and sin θ > 0
(b) sin θ < 0 and cot θ < 0
(c) csc θ < 0 and sec θ < 0
(d) sec θ < 0 and tan θ < 0

22. Find the quadrant containing θ if the given conditions are true.

Quadrant I
Quadrant II
Quadrant III
Quadrant IV

(a) tan θ < 0 and cos θ > 0
(b) sec θ < 0 and tan θ < 0
(c) csc θ < 0 and cot θ < 0
(d) cos θ < 0 and csc θ < 0

23. Use fundamental identities to find the values of the trigonometric functions for the given conditions.

tan θ = -3/4 and sin θ > 0

24. Use fundamental identities to find the values of the trigonometric functions for the given conditions.

cot θ = 4/3 and cos θ < 0

25. Use fundamental identities to find the values of the trigonometric functions for the given conditions.

sin θ = -4/5 and sec θ > 0

26. Use fundamental identities to find the values of the trigonometric functions for the given conditions.

cos θ = 1/2 and sin θ < 0.

Reference no: EM13975915

Questions Cloud

Define cost shifting in your own words. : QUESTIONS: Define Cost Shifting in your own words. * Do you think that it is a fair practice or should it be legally banned?

Describe the life cycle of midlatitude cyclones : Describe the life cycle of midlatitude cyclones (including how and why the systems develop, move, mature, and dissipate) and the resulting weather elements associated with them and examine the general circulation of the (global) atmosphere (semi-p..

Write kirchhoffs loop rule relation for a loop : Let I1 be the branch current though R1, I2 be the branch current through R2, and I3 be the branch current through R3. Write Kirchhoff?s loop rule relation for a loop that travels through battery 1, resistor 1, and resistor 3. (Use a clockwise curr..

Calculating federal income tax liability for the individual : Explain qualification of dependency as it relates to claiming dependent exemptions from taxable income.

Find values of six trigonometric functions for given angle : Find the values of the six trigonometric functions for the angle θ. Find the values of the six trigonometric functions for the angle θ. Assume a = 1, c = 4.

Explain what crimes svoboda and robles each committed. : Explain any defenses that Svoboda and Robles could raise and the likely success of the defense.

Find the total electric charge inside the cube : Find the total electric charge inside the cube. In the charge configuration below, find the location (that is, x coordinate) where the electric field by the two point charges shown on the axis is zero. Note that O is the origin.

What should it professionals know about iot and why : What should IT professionals know about IoT and why? Provide a thorough explanation to this question after review the above links and Refer to the 12 response attached below and explain which response you found most helpful to week #1 assignment an..

What costs should the decision maker consider as sunk cost : Relevant and sunk costs McKinnon Company's plant manager is considering buying a new grinding machine to replace an old grinding machine or overhauling the old one to ensure compliance with the plant's high-quality standards. The following data ar..

User Account

All Pages