Reference no: EM13836107

Part 1:

1. Find the volume V of the solid whose base is the circle x² + y² = 9 and whose cross sections perpendicular to the x-axis are triangles whose height and base are equal.

2. Find the volume V of the solid whose base is the semicircle y = √ 16 - x², where -4 ≤ x ≤ 4 and whose cross sections perpendicular to the x-axis are squares.

3. The base of the solid is the region enclosed by y = x² and y = 3. The cross sections perpendicular to the y-axis are rectangles of height y³. Compute the volume of the solid.

4. Find the volume V of the solid whose base is the region ιxι + ιyι ≤ 8 and whose cross sections perpendicular to the y-axis are semicircles (with diameter along the base).

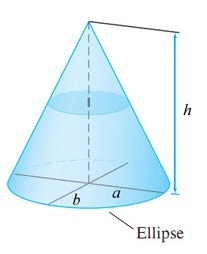
5. The area of an ellipse is πab, where a and b are the lengths of the semimajor and semiminor axes. Compute the volume of a cone of height h = 60 whose base is an ellipse with semimajor axis a = 12 and semiminor axis b = 10.

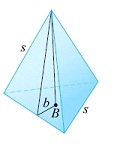
6. Find the volume V of a regular tetrahedron whose face is an equilateral triangle of side length 6.

Part 2:

1. Calculate the volume of the solid obtained by revolving the region under the graph of f(x) = √ x + 5 about the x-axis over the interval.

2. Find the volume V of the solid obtained by rotating the region under the graph of the function f(x) = e^x about the x-axis over the interval.

3. Find the volume of the solid obtained by rotating the region enclosed by the curves y = x² + 9 and y = 17 - x² about the x-axis.

4. Find the volume V of the solid obtained by rotating the region enclosed by the graphs x = y⁹ and x = ⁹√ y about the y-axis over the interval.

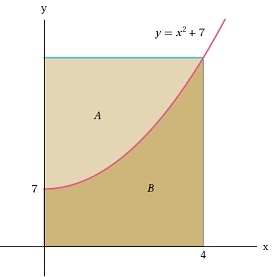
5. Find the volume of the solid obtained by rotating the region A in the figure below about the line y = 7.

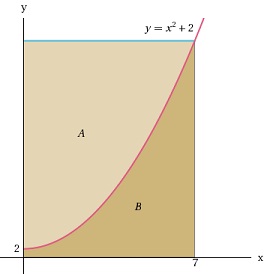
6. Find the volume of the solid obtained by rotating the region A in the figure below about the line x = -1.

7. Find the volume of the solid obtained by rotating the region enclosed by the graphs about the given line.

y = 2√x , y = x, about y = 4.