Reference no: EM132614342

Question 1. Find the derivative of the following functions:

(a) 4e^x sin^-1(x)

(b) ln(ln(ln(x)))

(c) arccos(x³ + x)

(d) tan-1(sin x)

Question 2. (a) Integrate xsinh x with respect to x .

(b) Find the moment of inertia and the radius of gyration w.r.t. the origin (0,0) of a system which has masses at the points given:

Mass	6	5	9	2
Point	(-3,0)	(-2,0)	(1,0)	(8,0)

(c) Use Leibnitz's theorem to find yn , if y = x^n-1 log x .

Question 3. (a) Prove that the hyperbolic identity cosh² x -sinh² x =1

(b) Find the first four derivatives for R(t) = 3t² + 8t^1/2 + e^t.

(c) Find the second derivative for R(t) = 3t² + 8t^1/2 + e^t

(d) Evaluate ₀∫^Π/9cos( 3x - Π/6 )dx .

Question 4. (a) Sketch the curve

y = x + x²

(b) Find the volume of solid of revolution formed by rotating the area enclosed by the curve y = x + x² , the x - axis and the ordinates x = 2 and x = 3 through one revolution about the x - axis.

(c) Find the area between the line y = 3x + 2 and the x -axis from x = 1 to x = 3.

(d) The graphs of y = x² + 2x + 3 and y = 2x² + x +1are shown below. 

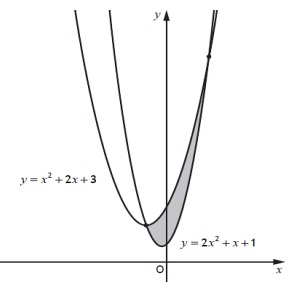
The graphs intersect at the points where x = -1 and x = 2 .

(i) Express the shaded area, enclosed between the curves, as an integral.

(ii) Evaluate the shaded area.

Question 5. (a) Given that f (x, y) = x⁴y³z⁶ find ∂⁶ f/∂y∂z²∂y∂x²

(b) Evaluate ∫3x² + 2x + 7/x² +1 dx

(c) Find ∫ x²e^xdx.