Reference no: EM133124282

Question 1: Are the vectors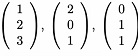linearly independent in R³? Do they span R³? Explain why.

Determine whether the following vectors are linearly independent in C [1, ∞]. Explain why.

(a) 10, cos²(x), cos(2x).
(b) e^x + e^-x, e^x - e^-x, 5.
(c) ln(2x), log3(5x), 2.

Question 2: Let fy(y) = Π/((y-α)² + β²) -∞< y < ∞ and constants α > 0 and β > O.

Verify that f is the pdf of a continuous random variable Y.

Show that for this distribution, the first moment about the origin does not exist.

Question 3: Suppose the random variable Y has probability density function fy(y) = 1/2 e^-|Y| for -∞ < y < ∞.

a. Show that its moment-generating function is given by My (t) = 1/1-t²

b. Also find the variance of the distribution of this random variable by expanding the moment-generating function as an infinite series and reading off the necessary coefficients.