Find the value of the linear correlation coefficient

Assignment Help Basic Statistics

Reference no: EM131606614

Question 1:

The eruption height and the time interval after eruption of a geyser were measured and are shown below. Answer parts a-c.

Height (x)	Interval after (y)
130	82
150	77
115	40
110	84
100	55
110	84
115	91
140	73

view a table of critical values for the correlation coefficient.

a. Find the value of the linear correlation coefficient r.

b. Find the critical values of r from the table showing the critical values for the Pearson correlation coefficient using α = 0.05.

c. Is there sufficient evidence to conclude that there is a linear correlation between the two variables?
A. Yes, because the absolute value of the correlation coefficient is less than the critical value.
B. Yes, because the absolute value of the correlation coefficient is greater than the critical value.
C. No, because the absolute value of the correlation coefficient is less than the critical value.
D. No, because the absolute value of the correlation coefficient is greater than the critical value.

Question 2:

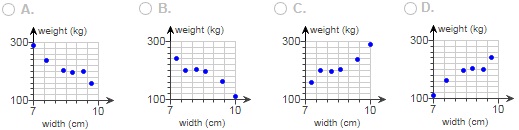
Listed below are the overhead widths (in cm) of seals measured from photographs and the weights (in kg) of the seals. Construct a scatterplot, find the value of the linear correlation coefficient r, and find the critical values of r using α = 0.01. Is there sufficient evidence to conclude that there is a linear correlation between overhead widths of seals from photographs and the weights of the seals?

Overhead Width	Weight
7	111
7.6	163
9.7	243
9.3	200
8.8	204
8.4	195

view a table of critical values for the correlation coefficient.

Construct a scatterplot. Choose the correct graph below.

Question 3:

The data below shows height (in inches) and pulse rates (in beats per minute) of a random sample of women. Answer parts a-c.

height (x)	pulse rate (y)
64.2	76
67.4	73
61.1	88
60.7	62
60.4	74
62.6	67
60.5	84
61.4	60
67.9	69
60.5	65
67.9	81
64.5	80

a. Find the value of the linear correlation coefficient r.
b. Find the critical values of r from the table showing the critical values for the Pearson correlation coefficient using α = 0.05.
c. Is there sufficient evidence to conclude that there is a linear correlation between the two variables?
A. Yes, because the absolute value of the correlation coefficient is greater than the critical value.
B. Yes, because the absolute value of the correlation coefficient is less than the critical value.
C. No, because the absolute value of the correlation coefficient is greater than the critical value.
D. No, because the absolute value of the correlation coefficient is less than the critical value.

Question 4:

A sample of 60 women is obtained, and their heights (in inches) and pulse rates (in beats per minute) are measured. The linear correlation coefficient is 0.263 and the equation of the regression line is y^ = 17.7 + 0.940x, where x represents height. The mean of the 60 heights is 63.2 in and the mean of the 60 pulse rates is 77.5 beats per minute. Find the best predicted pulse rate of a woman who is 68 in tall. Use a significance level of α = 0.01.

Question 5:

Listed below are systolic blood pressure measurements (in mm Hg) obtained from the same woman. Find the regression equation, letting the right arm blood pressure be the predictor (x) variable. Find the best predicted systolic blood pressure in the left arm given that the systolic blood pressure in the right arm is 80 mm Hg. Use a significance level of 0.05.

Right Arm	Left Arm
100	175
99	168
91	182
79	142
78	143

The regression equation is y^ = __ + __x.

Question 6:

Use the value of the linear correlation coefficient r to find the coefficient of determination and the percentage of the total variation that can be explained by the linear relationship between the two variables.

r= 0.2

What is the value of the coefficient of determination?

What is the percentage of the total variation that can be explained by the linear relationship between the two variables?

Question 7:

Eight different medical students took blood pressure measurements of the same patient and the results are listed below.

The regression equation is y^ = -16.883311 + 0.783796x and the standard error of the estimate is 2.6958. Assume that the necessary conditions of normality and variance are met, and answer parts a and b.

systolic (x)	diastolic (y)
135	87
130	85
140	97
136	88
120	78
129	83
125	84
130	82

a. Find the predicted diastolic reading given that the systolic reading is 134.
b. Find a 95% prediction interval estimate of the diastolic reading given that the systolic reading is 134.

Question 8:

When generating random digits, we can test the generated digits for goodness-of-fit with the distribution in which all of the digits are equally likely. What does an exceptionally large value of the χ² test statistic suggest about the goodness-of-fit? What does an exceptionally small value of the χ² test statistic (such as 0.002) suggest about the goodness-of-fit?

Choose the correct answer below.

A. Large test statistic - fit is not good. Small test statistic - fit is not good.
B. Large test statistic - fit is not good. Small test statistic - fit is extremely good.
C. Large test statistic - fit is extremely good. Small test statistic - fit is not good.
D. Large test statistic - fit is extremely good. Small test statistic - fit is extremely good.

Question 9:

Conduct the hypothesis test and provide the test statistic, critical value and P-value, and state the conclusion.

A person purchased a slot machine and tested it by playing it 1,270 times. There are 10 different categories of outcomes, including no win, win jackpot, win with three bells, and so on. When testing the claim that the observed outcomes agree with the expected?

frequencies, the author obtained a test statistic of χ² = 19.143. Use a 0.05 significance level to test the claim that the actual outcomes agree with the expected frequencies. Does the slot machine appear to be functioning as expected?

The test statistic is __.

Question 10:

Conduct the hypothesis test and provide the test statistic, critical value and P-value, and state the conclusion.

A person randomly selected 100 credit card purchases and recorded the cents portions of those amounts. The table below lists those cents portions categorized according to the indicated values. Use a 0.025 significance level to test the claim that the four categories are equally likely. The person expected that many checks for whole dollar amounts would result in a disproportionately high frequency for the first category, but do the results support that expectation?

Cents portion	Number
0-24	32
25-49	22
50-74	20
75-99	26

The test statistic is___.

Question 11:

Hypothesis tests based on this section, "Contingency Tables", are always what type of hypothesis test?

Choose the correct answer below.
A. Right-tailed
B. Two-tailed
C. Left-tailed

Question 12:

Winning team data were collected for teams in different sports, with the results given in the table below. Use the TI-83/84 Plus results at a 0.05 level of significance to test the claim that home/visitor wins are independent of the sport.

TI-83/84 PLUS

χ²-test

χ² =7.092988473
P = 0.0689922371
df = 3

	Basketball	Baseball	Hockey	Football
Home team wins	111	46	62	39
Visiting team wins	72	55	51	41

Question 13:

The data in the accompanying table summarizes results from tests of the accuracy of mammograms. Use a 0.05 significance level to test the claim that whether the subject has a tumor is independent of the mammogram indication. What do the results suggest about the effectiveness of mammograms?

	Mammogram Indicated Tumor	No Tumor
Subject had a tumor	13	44
Subject did not have a tumor	18	23

Are mammograms effective?

A. Yes, there is not sufficient evidence to reject the claim of independence.
B. No, there is sufficient evidence to reject the claim of independence.
C. No, there is not sufficient evidence to reject the claim of independence.
D. Yes, there is sufficient evidence to reject the claim of independence.

Question 14:

Below are the results of a trial involving an experimental vaccine for children.

	Developed flu	Did not develop flu
Vaccine treatment	14	95
Placebo	1056	437

Use a 0.05 significance level to test for independence between the columns and rows.

Does the vaccine appear to be effective question mark
A. Yes, because the test statistic is less than the critical value.
B. No, because the test statistic is less than the critical value.
C. Yes, because the test statistic is greater than the critical value.
D. No comma because the test statistic is greater than the critical value.

Question 15:

This table summarizes results from an experiment in which subjects were first classified as smokers or nonsmokers, then they were given a treatment, then later they were again classified as smokers or nonsmokers. How many subjects appear to be unaffected by the treatment one way or the other?

Before Treatment

Smoke Don't Smoke

After Treatment

Smoke 414 8

Don't Smoke 358 174

How many subjects were unaffected?

Question 16:

Subjects have athlete's foot on each of their feet. For each subject, one foot is given a fungicide, the other a placebo. Using a 0.05 significance level, test the effectiveness of the treatment.

		Fungicide Treatment
		Cure	No Cure
Placebo	Cure	9	20
Placebo	No Cure	24	45

Is there sufficient evidence to conclude that the fungicide is effective? Why? Choose the correct answer below.

A. No, because the test statistic does not exceed the critical value.
B. No, because the test statistic exceeds the critical value.
C. Yes, because the test statistic exceeds the critical value.
D. Yes, because the test statistic does not exceed the critical value.

Attachment:- Table of critical values for the correlation coefficient.pdf

Reference no: EM131606614

Questions Cloud

How would that affect any cpfr activities : Please explain how CPFR would reduce or eliminate ethical and legal problems in the supply chain of Feets. Many of the Feets vendors are offshore.

Analyze expected changes in interest rates : Monitoring the Cost Of Money- Interest Rates. More importantly where do you find the information to analyze expected changes in interest rates?

Developing the employee schedules for the retail stores : What are the parameters and considerations that must be made when developing the employee schedules for the retail stores at Feets.

Surfing school on the north shore of oahu : Nick runs a surfing school on the North Shore of Oahu. He has two inputs: surfboards, which he rents from a local shop for $15 per day

Find the value of the linear correlation coefficient : Find the value of the linear correlation coefficient r and find the critical values of r from the table showing the critical values

What should you and your manager do next : Recommendations. What should you and your manager do next? Support your recommendations with evidence from your financial analysis.

Prepare income tax return for the year ended : ACC00132-2017-2 Taxation Major Assignment. Your client Stefan comes to see you in August 2017, asking to prepare his income tax return for the year ended

Determine effect on equilibrium price of the introduction : A monopolist faces an inverse demand function p=100-4q and her total cost of production is c=20q.

The creation of the faa and icao : What were the driving forces behind the creation of the FAA and ICAO? This question is pertaining to the airline versus FAA safety responsibilities.

User Account

All Pages