Reference no: EM13254450

1. Find the unique factorisation of 1176.

2. Calculate the following:

(a) 228 div 119
(b) -10101 mod 333
(c) 230 x 91 mod 11

3. Prove that every number from the set {2, 4, 6, 8......., 26} can be written as the sum of at most 3 square numbers (A square number is a perfect square, e.g. 1 = 1², 4 = 2², 9 = 3³ etc.)

4. Prove: ∀k ∈ Z, [3|(k - 2) → 3|(k² - 1)].

5. Prove the following statement:

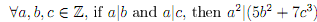
6. Consider the following statement:

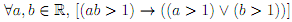
(a) Write the negation of the statement.

(b) Determine which of the original statement or the negation is true. Justify your answer.

7. Use a direct proof to show that

                                     1 + 2 + 3 + .........+ n = n(n+1)/2

(You might get some inspiration from the story of little Gauss who was given a similar problem to do in class. Gauss was asked to add the first hundred positive integers. He took no time at all to work it out! How did he do it? (clue in cartoon!) Apply a similar idea to your proof. Later in the course, we will use another method to prove the result).

8. Prove the following:

(a) For any integer a, a ≡ a (mod m), where m is a positive integer.
(b) For all integers a, b, c, if a ≡ b (mod m) and b ≡ c (mod m), then a ≡ c (mod m), where m is a positive integer.
(c) For all integers a and b, if a ≡ 2 (mod 4), and b is odd, then ab ≡ 2 (mod 4).

9. Are the following statements true or false? Prove the statement if it is true and give a counterexample if it is false.

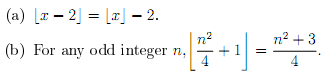
10.

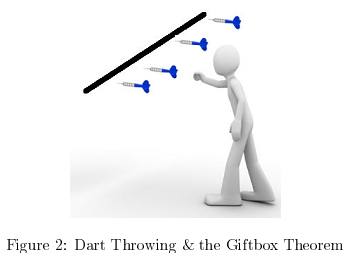
(a) Prove the Giftbox Theorem using the method of contradiction:

Suppose there are (n + 1) gifts and 71 gift boxes. Then some gift box must contain at least 2 gifts.

(b) Use the Giftbox Theorem to prove the following:

Suppose you have a line segment which is 1 metre long. You throw darts at the line segment and being a good shot, your dart lands on the line segment each time. You throw 11 darts in total. Show that there is a pair of darts with distance not greater than 10 cm. (Hint: divide the line segment into 10 intervals of length 10 cm each, then use the Giftbox Theorem!)