Reference no: EM132210388
Question 1
Consider the following problem
Maximize z = 4x1 + 5x2 + 3x3
Subject to
x1 + x2 + 2x3 ≥ 20
15x1 + 6x2 - 5x3 ≤ 50
x1 + 3x2 + 5x3 ≤ 30
and
x1 ≥ 0, x2 ≥ 0, x3 ≥ 30
Work through the simplex method step by step to demonstrate that this problem does not posses any feasible solutions.
Question 2
The Build-Em-Fast Company has agreed to supply its best customer with three widgets during each of the next 3 weeks; even through producing them will require some overtime work. The relevant production data are as follows:
|
Week
|
Maximum
Production,
Regular Time
|
Maximum
Production,
Overtime
|
Production Cost
Per Unit,
Regular Time
|
|
1
2
3
|
2
3
1
|
2
2
2
|
$300
$500
$400
|
The cost per unit produced with overtime for each week is $100 more than for regular time. The cost of storage is $50 per unit for each week it is stored. There is already an inventory of two widgets in hand currently, but the company does not want to retain any widgets in inventory after the 3 weeks.
Management wants to know how many units should be produced in each week to minimize the total cost of meeting the delivery schedule.
(a) Formulate this problem as a transportation problem by constructing the appropriate parameter table.
(b) Obtain an optimal solution.
Question 3
Consider the transportation problem having the following parameter table.
|
|
|
Destination
|
Supply
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
Source
|
1
2
3
4
5
|
13
14
3
18
30
|
10
13
0
9
24
|
22
16
M
19
34
|
29
21
11
23
36
|
18
M
6
11
28
|
0
0
0
0
0
|
5
6
7
4
3
|
|
Demands
|
|
3
|
5
|
4
|
5
|
6
|
2
|
|
Use each of the following criteria an initial BF solutions Compare the values of the objective function for these solutions.
(a) Northwest Corner Rule
(b) Vogel's approximation method.
Question 4
The coach of an age group swim team needs to assign swimmers to a 200-yard medley relay team to send to the junior Olympics. Since most of his best swimmers are very fast in more then one stroke, it is not clear which swimmer should be assigned to each of the four strokes. The five fastest swimmers and the best times (in seconds) they have achieved in each of the strokes (for 50 yards) are:
|
Stock
|
Carl Chris David Tony Ken
|
|
Backstroke
Breaststroke
Butterfly
Freestyle
|
37.7 32.9 33.8 37.8 35.4
43.4 33.1 42.2 34.7 41.8
33.3 28.5 38.9 30.4 33.6
29.2 26.4 29.6 28.5 31.1
|
The coach wishes to determine how to assign four swimmers to the four different strokes to minimize the sum of the corresponding best times.
(a) Formulate this problem as an assignment problem.
(b) Obtain as optimal solution.
Question 5
Consider the following network, where each number along a link represents the actual distance between the pair of nodes connected by that link. The objective is to find the shortest path from origin to destination.
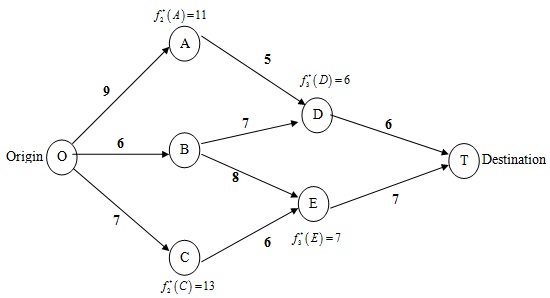
(a) What are the stages and states for the dynamic programming formulation of this problem?
(b) Use dynamic programming to solve this problem by manually constructing the usual tables for n = 3, n = 2, and n = 1.