Reference no: EM1398685

Question 1. Consider a competitive labor market with a continuum of workers. Each worker is characterized by his productivity θ ∈{θ_H, θ_L}. The proportion of workers with type θ_H is α. Before applying for a job, each worker chooses the level of his education e ≥ 0. The education is costly and has no effect on productivity. If a worker with productivity θ gets an education e and a wage w his payoff is

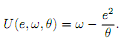
If a worker decides not to participate in the job market, he gets zero payo.

a) Argue that in the competitive market, a wage paid to a worker equals to his expected productivity (conditional on all the information about this worker known to rms).

b) What is the dierence between separating and pooling equilibria in this model? Find the separating equilibrium with the lowest possible education level for the high type.

c) What is the largest level of education that can be chosen by workers with productivity H in equilibrium in this model?

d) Find a pooling equilibrium in this model.

e) Suppose the equilibrium that you found in b) is played. The government comes up with a bill that prohibits wage discrimination based on education (i.e. holding other publicly observable workers' characteristics the same, rms can not oer dierent wages to people with dierent education levels). To pass the bill, the government holds a referendum in which only workers can vote. Assuming that voters vote sincerely, i.e. voters pick an alternative that gives them the highest payo, and that a simple majority is required for passing the bill, derive a necessary and sucient condition for passing this bill (the condition must be formulated in terms of fundamentals of the model)

Question 2. Firm A (the \acquirer") is considering taking over rm T (the \target"). It does not know rm T's value, it believes that this value, when rm T is controlled by its own management, is at least $0 and at most $100, and assigns equal probability to each of the 101 dollar values in this range. Firm T will be worth 50% more under rm A's management than it is under its own manage ment. Suppose that rm A bids y to take over rm T, and rm T is worth x (under its own management). Then if T accepts A's oer, A's payo is 3/2x - y and T's payo is y, if T rejects A's oer, A's payo is 0 and T's payo is x:

Model this situation as a Bayesian game in which rm A chooses how much to oer and rm T decides the lowest oer to accept. Find the Nash equilibria of this game. Explain why the logic behind the equilibrium is called adverse selection.

Question 3. John Harsayni showed that a mixed strategy equilibrium of a perfect information game can be thought of as an approximation to an equilbrium (i.e. Bayesian NE) of a game where each player has a slight amount of incomplete information about the exact preferences of the other players. Consider the following Bayesian game, with payos as given below:

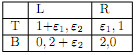
Nature chooses "1 and "2 independently, and both of these are uniformly distributed on the interval [-k, k] where k < 0:5: Player i is informed of the realization of "i, but not of "j , j = i: Players then choose actions simultaneously.

a) Solve for an Nash equilibrium of this game when k = 0:

b) Solve for a Bayesian NE when k > 0, k < 0:5: What is the probability assigned by player i to the event that his opponent plays his rst action in this BNE?

c) What do the probabilities in (b) converge to when k -> 0: Interpret your results.

Question 4. Consider the following simpli ed version of a game of poker. There are two players and three cards in a deck: Jack, Queen and King of spades. Player 1 always gets a Queen. Player 2 gets a Jack with probability 0.5 or a King with probability 0.5. In the rst round, player 2 can either Raise or See. If he plays See, the game ends and players see each other's cards. Whoever has a lower card has to pay $1 to the opponent. If player 2 played Raise, the game continues to the second round in which player 1 can either play Pass or Meet.

If he plays Pass, the game ends and player 1 has to pay $1 to player 2. If player 1 plays Meet, the game ends and the players see each other's cards. Whoever has a lower card has to pay $2 to the opponent.

a) Formulate the game in the extensive form and draw a tree of the game.

b) What is an assessment in this game? Write it down in a parametric form (i.e. by denoting unknown strategies and beliefs by some letters).

c) Under what conditions on the belief system does player 1 play Meet?

d) Solve for all weak sequential equilibria of this game and classify each equilibrium as pooling, partially separating or fully separating.