Reference no: EM132372876

Assignment - Methods of Applied Mathematics Problems

Part A -

Recall that the columns of a matrix A are linearly dependent if and only if the homogeneous equation Ax = 0 has a non-trivial solution. Also, a vector y is in the span of the columns if and only if the inhomogeneous equation Ax = y has a solution.

1. Show that if p is a particular solution of the equation Ax = b, then every other solution is of the form x = p + z, where Az = 0.

2. Consider the matrix

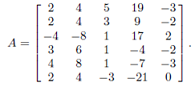
Use Matlab to find the reduced row echelon form of the matrix. Use this to find the rational basis for the solution of the homogeneous equation Az = 0. Check this with the Matlab solution. Write the general solution of the homogeneous equation.

3. Let A be the matrix given above. Use Matlab to find an invertible matrix E such that EA = R is in reduced echelon form. Find the determinant of E.

4. Consider the system Ax = b, where A is as above, and

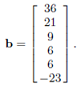
Find the reduced echelon form of the matrix A augmented by the column -b on the right. Use this to find the rational basis for the solution of the homogeneous equation involving the augmented matrix. Use this to find the general solution of the original inhomogeneous equation.

5. Consider a system of 6 linear equations in 5 unknowns. It could be over-determined, that is, have no solutions. Or it could have special properties and be under determined, that is, have many solutions. Could it be neither, that is, have exactly one solution? Is there such an example? Answer this question, and prove that your answer is correct.

6. Consider a system of 5 linear equations in 6 unknowns. Could it have exactly one solution? Is there such an example? Answer this question, and prove that your answer is correct.

Part B -

1. If A is a square matrix and f is a function defined by a convergent power series, then f(A) is defined. Show that if A is similar to B, then f(A) is similar to f(B).

2. Show that

exp(t(D + N)) = exp(tD)_m=0Σ^p-1(1/m!)N^mt^m.

Use this to describe the set of all solutions x = exp(tA)z to the differential equation

dx/dt = Ax.

with initial condition x = z when t = 0.

3. Take

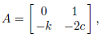
where k ≥ 0 and c ≥ 0. The differential equation describes an oscillator with spring constant k and friction coefficient 2c. Find the eigenvalues and sketch a typical solution in the x₁, x₂ plane in each of the following cases: over damped c² > k > 0; critically damped c² = k > 0; under damped 0 < c² < k; undamped 0 = c² < k; free motion 0 = c² = k.

4. If A = PDP^-1, where the diagonal matrix D has diagonal entries λ_i, then f(A) may be defined for an arbitrary function f by f(A) = Pf(D)P^-1, where f(D) is the diagonal matrix with entries f(λ_i). Thus, for instance, if each λ_i ≥ 0, then √A is defined. Find the square root of