Reference no: EM132155878

Assignment -

1. Model fitting

You have been given the task of describing the dependence of a system's performance T (time in milliseconds) on a parameter p. The following data is available.

p	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
T(p)	248	129	91	79	74	78	85	98	110	125	144	166	188	215	241

From the log-log plot you guess that the performance can be modelled by T_ab(p) = ap² + b/p, where a, b are some constants. Now, you need to find such constants a, b that the model Tab fits the given data best.

(a) Let R(a, b) denote the residual sum of squares between data points (p, T(p))_p=1,...,15 and the model T_ab. Show that R(a, b) has unique stationary point (a₀, b₀).

(b) Find the values of a₀ and b₀ rounded to nearest integers.

(c) Justify that the stationary point (a₀, b₀) is the global minimum of R(a, b).

You can use the following approximations: _p=1∑¹⁵p⁴ ≈ 1.78 · 10⁵, _p=1∑¹⁵p^-2 ≈ 1.58, _p=1∑¹⁵p²T(p) ≈ 2.09 · 10⁵, _p=1∑¹⁵p^-1T(p) ≈ 512.

2. Skatepark design

A new skatepark to be built in the area R = {(x, y) ∈ R² : x² + y² < 1}. Its design is described by a continuous function h(x, y) which corresponds to the elevation of the surface at point (x, y). There are certain requirements that the skatepark should satisfy:

(i) h(x, y) = 0 for any point on the perimeter, i.e. for any (x, y) such that x² + y² = 1;

(ii) the function h has exactly one local minimum and one local maximum in R;

(iii) there are no other stationary points of h in R.

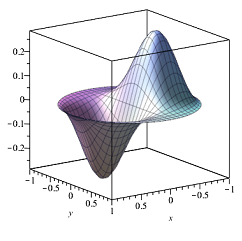
(a) Is it possible to find h satisfying just the requirements (ii) and (iii) which has the form h(x, y) = ax² + by² + cxy + dx + ey + f, where a, b, c, d, e, f are constants?

(b) Construct some suitable h(x, y) that (i), (ii), (iii) are satisfied. Justify your answer.

Hint: take h to be of the form h(x, y) = (x² + y² - 1)g(x, y) for some appropriate function g. For example, you can try g(x, y) = p(x)q(y) or something else.

3. Lucky numbers

A four-digit number is lucky if the sum of its first two digits equals the sum of the last two digits (Note that all digits are from {0, 1, . . . , 9}, except the first one which is non-zero).

(a) How many four-digit lucky numbers are there?

(b) How many four-digit lucky numbers do not contain repeating digits? For example, the lucky numbers 1515 and 1551 are not allowed.

4. Analysis of medical data

A deadly epidemic virus has spread over a city. Scientists invented two drugs α and β to reduce the activity of the virus. They conducted the following test on a sample of infected people. The drug α was given to 70% of the sample and the drug β was given to 60% of the sample (everyone was given at least one drug, but some people used both drugs). The test results show that 60% of the sample managed to recover. From a survey conducted among the recovered people you know that 40% of them used the drug α only, 40% of them used the drug β only.

(a) Consider the uniform probability space where the sample space S is the set of people participating in the test. Let A, B ⊂ S correspond to people taking drugs α, β, respectively and let R ⊂ S correspond to recovered people. Write the information given above in terms of probabilities (or conditional probabilities) of A, B, A¯, B¯, R, their intersections and unions.

(b) Compute Pr(R | A ∩ B¯), Pr(R | B ∩ A¯), Pr(R |A ∩ B). Which immunisation strategy (drug α, drug β or both drugs) do you suggest based on the results of the test?

5. Random bushwalk

A bushwalker starts a four-day hike from point (0, 0) (on the 2D plane). During the journey, he can either spend the whole day at the same point (a, b) or move to any of the neighbouring points: (a + 1, b), (a - 1, b), (a, b + 1), (a, b - 1). Assume that every day he chooses one of these five options uniformly at random and independently of the past.

(a) Find the probability that the bushwalker returns to the starting point (0, 0) at the end of the four-day hike.

(b) Let (X, Y) be the coordinates of the bushwalker after four days. Compute E(X²+Y²).

(c) Are X and Y independent random variables? Justify your answer.