Reference no: EM13796344
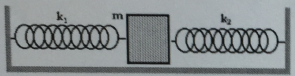
Q1. A) In the figure below, k1= 5 N/m, k2 = 15 N/m and mass in = 2 Kg. Find the oscillation time period of the spring (in seconds).
Q1. B) A Jack-In-The-Box is built with a spring that has a spring constant 70N/m. How hard does the spring push when you compress it from 40 cm long down to 15 cm long? (i.e, find the restoring Force in Newton's).
Q2: Nick, who weighs 75 kg and stands 1.8 meters tall (6 feet), wants to go bungee lumping, but doesn't have a bungee cord. He finds a 15 m long, flexible spring (with a spring constant of 30 N/m) in his garage, which he decides should work just as well. He takes the spring to a nearby bridge that is 50 meters above the ground, attaches one end to the bridge and the other to his leg and jumps off. After bouncing around violently for a while, he finally comes to rest. How far above the ground is his head (in meters)?
Q3: One mole of Uranium has a mass of 238 grams. The density of Uranium is 18.68 grams/cm3. Suppose you have a bar of Uranium that is 0.5 m long, with a square cross-section. The short side measures 0.1cm. You hang the bar from a support (with the long end vertical) and attach a 40 Kg to the bottom and observe that the bar elongates by 0.5 cm. I now remove the mass and put the bar back on a table. I strike a spoon on the table, and immediately place it against one of the square faces of the bar. How long does it take before the sound Is picked up (say, by a microphone) at the opposite face of the bar? (You may assume that the atoms of Uranium are arranged in a cubic array.)