Reference no: EM132400447

Question 1: An inner product on R³ is given by

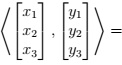
(x1+x2+x3)(y1+y2+y3)+(x1+2x2+4x3)(y1+2y2+4y3)+(x1+3x2+9x3)(y1+3y2+9y3).

(a) Verify that this inner product is commutative, linear in each coordinate, and positive definite.

(b) Using this inner product instead of the dot product, find an orthonormal basis for R3 using the corresponding analogue of Gram-Schmidt.

(c) Let W be the subspace of R³ consisting of all vectors in the plane

x + y + z = 0.

Find ω ∈ W minimizing

where the magnitude of any vector v ∈ R³ is defined to be √(v, v).

Question 2. Let V be equal to the vector space of integrable real-valued functions with domain [-1, 1]. An inner product on V is given by

(f, g) = ∫_-1¹ f(x)g(x) dx.

(a) Let W be the subspace of V spanned by f₀, f₁, f₂, and f₃, where f₀(x) = 1, f₁(x) = cos(πx), f₂(x) = cos(2πx), f₃(x) = cos(3πx). Find an orthonormal basis for W with respect to the given inner product.

(b) Let f ∈ V be the function defined by f (x) = x². Find the orthogonal projection of f onto W with respect to the given inner product, then plot both functions in the same coordinate system.