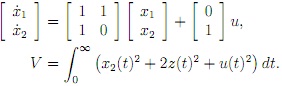Reference no: EM131486630

Instructions: This is an open-book, open-note exam. Do not discuss this exam with anyone throughout the exam period.

Question 1. (a) Given constant matrices A ∈ R^n×n and C ∈ R^p×n, show that (A, C) is observable if and only if (A, C^T C) is observable.

(b) If Φ denotes the state transition matrix for the system x^· (t) = A(t)x(t), show that V (t) = Φ(t, t₀)QΦ^T(t, t₀) is a solution to the equation

d/dt.V (t) = A(t)V(t) + V(t)AT (t), V (t₀) = Q.

(c) Suppose that (A, C) is detectable, where A ∈ R^n×n and C ∈ R^p×n are constant matrices. Is (A + GC, C) detectable for any matrix G ∈ R^n×p? Prove or disprove by producing a counterexample.

Question 2. In the following, you have to explain why your solution is correct. For instance, you may refer to results given in the lecture notes or homework assignments that support your claim.

(a) Find the optimal feedback control law u(t) that minimizes the cost function

V = ₀∫¹((x^·(t) + u(t))² + 2x(t)².dt + x^·(1)²

subject to x¨ = u, as well as the minimum cost, where x(0) = 1, x^·(0) = 0. You may provide the formulas for the optimal control law and minimum cost in terms of matrix function(s) satisfying some differential equation(s). You do not have to solve the differential equation(s).

(b) Find the optimal feedback control law u(t) that minimizes the cost function

V = ₀∫¹u(t)^T u(t) dt + (x(1) - x_d)^T(x(1) - x_d)

subject to the LTV system x^· = A(t) x + B(t) u, as well as the minimum cost, where x(0) = x0, A(t) ∈ Rn×n and B(t) ∈ Rn×m are continuous in time t, and x_d ∈ Rⁿ is a constant vector. You may provide the formulas for the optimal control law and minimum cost in terms of matrix function(s) satisfying some differential equation(s). You do not have to solve the differential equation(s).

(c) Find a feedback control u that minimizes

V = ₀∫^∞(x²(t) + u²(t)) dt subject to x^· = xu.

Question 3. Consider the infinite horizon LQR problem with cost

V = ₀∫^∞(x(t)^TQx(t) + q¯z(t)²) + ru(t)²dt

subject to LTI system x^· = Ax + Bu, where x(t) = (x₁(t), x₂(t)) ∈ R², u(t) ∈ R, and

Z(s) = s²/(s² + s + 1) X₁(s) with s being the Laplace variable.

(a) Assuming that Q ≥ 0, q¯ > 0, and r > 0 are specified, obtain the optimal feedback control law that minimizes the above cost function and renders the closed-loop system stable by simply applying the (infinite horizon) LQR theory developed in the class notes. (State the conditions that would ensure a stabilizing controller.)

(b) After obtaining the general solution, apply it to the specific problem: