Reference no: EM131114306

Honors Examination: Algebra Spring 2006

1. A commutative ring A is called a local ring if it has a unique maximal ideal m.

(a) Show that if A is a commutative ring in which all the non-invertible elements of A form an ideal, then A is a local ring.

(b) Suppose A is a local ring with unique maximal ideal m. Show that m consists of all the non-invertible elements of A.

(c) Which of the following are local rings?

(i) The ring Z of integers.

(ii) The field C of complex numbers.

(iii) The polynomial ring C[x].

2. Define α = √2 + √3.

(a) Show that Q(α) = Q(√2, √3).

(b) Find the minimum polynomial of α over Q.

(c) Show that the extension Q(α)/Q is normal.

(d) Compute the Galois group of Q(α) over Q.

3. For this exercise, define

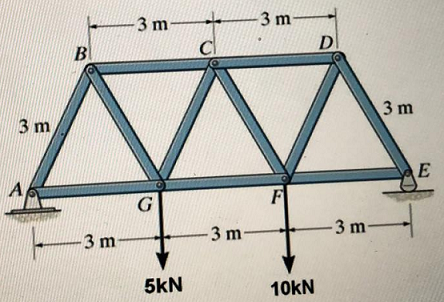
(a) Justify that R and S are rings with the usual matrix operations of addition and multiplication.

(c) Show that R is a field isomorphic to the field of complex numbers.

(b) Show that S is a division ring, meaning that each nonzero element of S has a multiplicative inverse.

(d) Show that S is not a field.

4. Let p be prime, n be a positive integer, and q = pⁿ.

(a) Show that if f (x), g(x) ∈ F_q[x] are distinct polynomials of degree at most q -1, then they are different as functions; i.e., there exists α ∈ F_q such that f (α) ≠ g(α).

(b) How many distinct functions are there from F_q to F_q? How many distinct polynomials are there of degree at most q- 1 with coefficients in F_q? Conclude that every function from F_q to F_q can be represented as a polynomial of degree at most q - 1 with coefficients in F_q.

(c) Show that if ψ is an automorphism of a finite field F_q, then ψ is of the form ψ(x) = x^{p^k}.

5. Let α ∈ S₅ be the permutation (12)(34).

(a) Determine the conjugacy class of α in S₅

(b) Determine all the elements of S₅ that commute with α.

(c) Determine the conjugacy class of α in A₅.

6. Given a field k, GL_n(k) denotes the group of all n x n invertible matrices with entries in k, and SL_n(k) denotes the group of all n x n matrices with determinant 1. Define PSL_n(k) to be the quotient of SL_n(k) by its center.

(a) Prove that SL_n(k) is a normal subgroup of GL_n(k).

(b) Prove that the center of GL_n(k) is the set of all matrices of the form λI_n where λ ∈ k.

(c) What is the center of SL_n(C)?

(d) Prove that PSL₂(F₂) ≅ S₃.

7. Consider the partition of { 1 , . . . , nm} given by

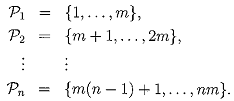
Let W be the subgroup of S_nm consisting of all permutations that preserve this partition; that is, for all σ ∈ W, if i, j ∈ P_k, then for some l, we have σ(i), σ(j) ∈ P_l.

(a) Show that W acts transitively on { 1 , . . . n m}, meaning that for any 1 ≤ i, j ≤ nm, there exists σ ∈ W such that σ(i) = j.

(b) Show that W has a normal subgroup N isomorphic to S_m x S_m x ··· x S_m, that fixes each P_i.

(c) Show that W/N is isomorphic to S_n.

 8. For which values of n between 3 and 6 is it possible to construct the regular n-gon by straightedge and compass? As usual, justify all your answers.

9. Let p be an odd prime and let e be an integer with 1 ≤ e ≤ p - 2 and gcd(p - 1, e) = 1.

(a) Prove there exists a positive integer d such that de ≡ 1 (mod p- 1) and 1 ≤ d ≤ p- 2.

(b) The Pohlig-Hellman Cryptosystem consists of two functions from Z_p to Z_p: enciphering is accomplished by the map

ε(m) = m^e (mod p)

and deciphering is accomplished by the map

D(m) = m^d (mod p).

Show that ε and D are inverse functions.

10. Let G be a group with 110 elements.

(a) Prove that G has exactly one Sylow 11-subgroup.

(b) Classify all the groups of order 110.

(c) Prove that G must contain a subgroup of order 10.

11. Let n be a positive integer, S_n the symmetric group on n characters, and V an n-dimensional vector space over a field k with basis {v₁, . . . , v_n}. Define an action of S_n on V via

σv_i = v_σ(i).

If φ: Sn → GL_n(k) is the corresponding matrix representation, prove that

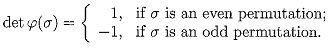
12. Let d ∈ Z be square-free and x, y ∈ Q.

(a) If d ≡ 3 (mod 4), then under what conditions is x + y√d an algebraic integer?

(b) Show that Z[√-5] is integrally closed.

(c) Show that Z[√-5] is not a Unique Factorization Domain.

(d) If d ≡ 1 (mod 4), then under what conditions is x + y√d an algebraic integer?

(e) Show that Z[√5] is not integrally closed.

(f) Show that Z[√5] is a Unique Factorization Domain.