Reference no: EM131243420
1) A block is launched with initial speed 2.5m/s up a frictionless, inclined ramp. It slides 47cm up the ramp before heading back down.
(a) Draw a free body diagram and clearly label your coordinate system and unit vector directions.
(b) Setup Newton's second law for each direction.
(c) What is the inclination angle, θ, of the ramp?
2) Starting from rest, a skier slides 100m down a 28° slope.
(a) Draw free body diagram and clearly specify your choice of coordinate system and unit vector di-rections when the coefficient of kinetic friction is θ.
(b) Setup Newton's 2nd law equations and solve for the acceleration.
(c) Draw a free body diagram and clearly specify your choice of coordinate system and unit vector directions for the case when the coefficient of friction is 0.17.
(d) Setup Newton's 2nd law for the situation in part c, and solve for the acceleration.
(e) How much longer does the run take if the coefficient of kinetic friction is 0.17 instead of θ? Hint: Don't forget about your kinematic equations for constant acceleration.
3) Two unfortunate climbers, roped together, are sliding freely down an icy mountainside. The upper climber (mass 75 kg ) is on a slope at 12° to the horizontal, but the lower climber (mass 62 kg ) has gone over the edge to a steeper slope at 38°.
(a) Draw a free body diagram of each climber and clearly specify your choice of coordinate system and unit vector directions.
(b) Assuming frictionless ice and a massless rope, what is the acceleration of the pair?
(c) The upper climber manages to stop the slide with an ice ax. After the climbers have come to a complete stop, what force must the ax exert against the ice?
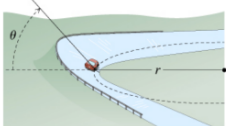
4) A car of mass m traveling at a speed vc enters a banked turn covered in ice. The road is banked at an angle θ, and there is no friction between the road and the car's tires as shown in the figure.
(a) Draw a free body diagram and clearly specify your choice of coordinate system and unit vector directions.
(b) Setup Newton's 2nd law equations.
(c) Find the magnitude of the normal force between the car and the road. Express your answer as a function of m, g,
(d) Find the magnitude of the acceleration of the car around the turn. Express your answer as a function of g and θ.
(e) Find the radius, r, of the curve needed so the car does not slip while going around the curve. Express your answer in terms of vc, g, θ.
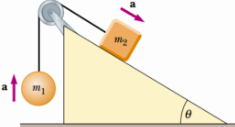
5) A ball of mass mi and block of mass m2 are attached by a lightweight cord that passes over a frictionless pulley of negligible mass, as shown in the figure. The block lies on a frictionless incline of angle θ.
(a) Draw a free body diagram for each object clearly labeling you coordinate systems and unit vector directions.
(b) Setup Newton's 2nd law equations for each object. Be sure to apply Newton's second law to each unit vector direction.
(c) Find the magnitude of the acceleration of the system. Express your answer in terms of ml, m2, θ, and g.
(d) Find the Tension T in the cord. Express your answer as a function of m1, m2, θ, and g.