Reference no: EM132346674
Probability & Statistics 1
1. The discrete random variable X has the following probability distribution.
|
X
|
1
|
3
|
5
|
7
|
|
P(X=x)
|
0.3
|
a
|
b
|
0.25
|
(i) Write down an equation satisfied by a and b.
(ii) Given that E(X) � 4, find a and b.
2. Ivan throws three fair dice.
(i) List all the possible scores on the three dice which give a total score of 5, and hence show that the probability of Ivan obtaining a total score of 5 is 1/36 .
(ii) Find the probability of Ivan obtaining a total score of 7.
3. The distance in metres that a ball can be thrown by pupils at a particular school follows a normal distribution with mean 35.0 m and standard deviation 11.6 m.
(i) Find the probability that a randomly chosen pupil can throw a ball between 30 and 40 m.
(ii) The school gives a certificate to the 10% of pupils who throw further than a certain distance.
Find the least distance that must be thrown to qualify for a certificate.
4. In a certain hotel, the lock on the door to each room can be opened by inserting a key card. The key card can be inserted only one way round. The card has a pattern of holes punched in it. The card has 4 columns, and each column can have either 1 hole, 2 holes, 3 holes or 4 holes punched in it.
Each column has 8 different positions for the holes. The diagram illustrates one particular key card with 3 holes punched in the first column, 3 in the second, 1 in the third and 2 in the fourth.
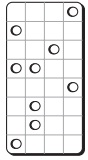
(i) Show that the number of different ways in which a column could have exactly 2 holes is 28.
(ii) Find how many different patterns of holes can be punched in a column.
(iii) How many different possible key cards are there?
5 Rachel and Anna play each other at badminton. Each game results in either a win for Rachel or a win for Anna. The probability of Rachel winning the first game is 0.6. If Rachel wins a particular game, the probability of her winning the next game is 0.7, but if she loses, the probability of her winning the next game is 0.4. By using a tree diagram, or otherwise,
(i) find the conditional probability that Rachel wins the first game, given that she loses the second,
(ii) find the probability that Rachel wins 2 games and loses 1 game out of the first three games they play.
6 (i) A manufacturer of biscuits produces 3 times as many cream ones as chocolate ones. Biscuits are chosen randomly and packed into boxes of 10. Find the probability that a box contains equal numbers of cream biscuits and chocolate biscuits.
(ii) A random sample of 8 boxes is taken. Find the probability that exactly 1 of them contains equal
numbers of cream biscuits and chocolate biscuits.
(iii) A large box of randomly chosen biscuits contains 120 biscuits. Using a suitable approximation, find the probability that it contains fewer than 35 chocolate biscuits.
7 The weights in kilograms of two groups of 17-year-old males from country P and country Q are displayed in the following back-to-back stem-and-leaf diagram. In the third row of the diagram, ... 4 � 7 � 1 . . . denotes weights of 74 kg for a male in country P and 71 kg for a male in country Q.
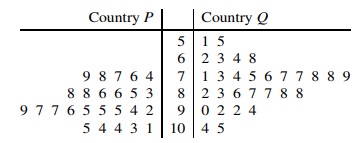
(i) Find the median and quartile weights for country Q.
(ii) You are given that the lower quartile, median and upper quartile for country P are 84, 94 and 98 kg respectively. On a single diagram on graph paper, draw two box-and-whisker plots of the data.
(iii) Make two comments on the weights of the two groups.